Giải câu 4 trang 53 SBT toán 8 tập 1 kết nối:

Đáp án đúng là: C

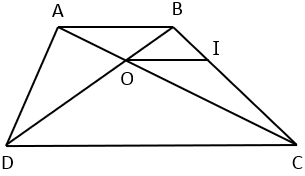
Qua O kẻ OI // AB // CD (I∈BC)

Trong ∆ABC có OI // AB theo định lí Thalès ta có:

$\frac{OA}{OC}=\frac{IB}{IC}; \frac{AO}{AC}{IB}{BC}$                 (1)

Trong ∆BCD có OI // DC theo định lí Thalès ta có:

$\frac{OB}{OD}=\frac{IB}{IC}; \frac{BO}{BD}{IB}{BC}$                 (2)

Từ (1) và (2) => $\frac{OA}{OC}=\frac{OB}{OD}$ (3)  và $\frac{AO}{AC}=\frac{BO}{BD}$

=> Khẳng định (1) sai và khẳng định (3) đúng.

Từ (3) suy ra: OA.OD=OB.OC => khẳng định (2) đúng.

Vậy có 2 khẳng định đúng.

Hoặc có thể sử dụng định lí Thalès cho hình thang ABCD ta có:

$\frac{OA}{OC}=\frac{OB}{OD}$ và $\frac{AO}{AC}=\frac{BO}{BD}$

=> OA.OD=OB.OC