A. CÂU HỎI TRẮC NGHIỆM

Câu 1 toán 8 tập 2 KNTT trang 78: Diện tích xung quanh của hình chóp tam giác đều, tứ giác đều bằng:

A. Tích nửa chu vi đáy và đường cao của hình chóp.

B. Tích nửa chu vi đáy và trung đoạn. 

C. Tích chu vi đáy và trung đoạn.

D. Tổng chu vi đáy và trung đoạn.

Đáp án: B

Câu 2 toán 8 tập 2 KNTT trang 78: Hình chóp tam giác đều có chiều cao h, thể tích V. Diện tích đáy S bằng

A. $S =\frac {h}{V}$

B. $S =\frac {V}{h}$

C. $S =\frac {3V}{h}$

D. $S =\frac {3h}{V}$

Đáp án: C

Câu 3 toán 8 tập 2 KNTT trang 78: Tổng số cạnh bên và cạnh đáy của một hình chóp tứ giác đều là

A. 4

B. 6

C. 8

D. 10

Đáp án: C

Câu 4 toán 8 tập 2 KNTT trang 78: Mặt đáy của hình chóp tứ giác đều là hình:

A. Tam giác đều

B. Hình bình hành

C. Tam giác cân

D. Hình vuông

Đáp án: D

Câu 5 toán 8 tập 2 KNTT trang 78: Một hình chóp tam giác đều có diện tích đáy bằng 4 cm, thể tích bằng 8 cm. Chiều cao của khối chóp bằng:

A. 8 cm

B. 9 cm

C. 4 cm

D. 6 cm

Đáp án: D

Câu 6 toán 8 tập 2 KNTT trang 78: Một đèn lồng có dạng hình chóp tứ giác đều có cạnh đáy bằng 15 cm, độ dài trung đoạn bằng 10 cm. Diện tích giấy dán kín bốn mặt bên của đèn lồng (coi như mép dán không đáng kể) là:

A. 200 $cm^{2}$

B. 300 $cm^{2}$

C. 400 $cm^{2}$

D. 500 $cm^{2}$

Đáp án: B

Câu 7 toán 8 tập 2 KNTT trang 78: Thể tích của hình chóp tứ giác đều S.MNPQ trong Hình 10.16 là:

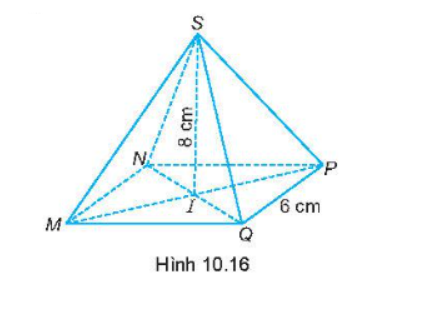
A. 288 $cm^{3}$

B. 14 $cm^{3}$

C. 96 $cm^{3}$

D. 48 $cm^{3}$

Đáp án: C

Câu 8 toán 8 tập 2 KNTT trang 79: Từ một mảnh bìa hình tam giác đều có cạnh 6 cm, gấp theo các nét đứt ta được một hình chóp tam giác đều (H.10.17). Hình chóp tam giác đều này có cạnh bên bằng

A. 6cm

B. 3 cm

C. 9 cm

D.  $\frac{3\sqrt{3}}{2}$ cm

Đáp án: B

Câu 9 toán 8 tập 2 KNTT trang 79: Một hình chóp tứ giác đều có thể tích bằng 64 cm, chiều cao bằng 12 cm. Độ dài cạnh đáy là

A. 16 cm

B. 8 cm

C. 4 cm

D. 10 cm

Đáp án: C

Câu 10 toán 8 tập 2 KNTT trang 79: Một khối gỗ (H.10.18) gồm đế là hình lập phương cạnh 9 cm và phần trên là một hình chóp tứ giác đều. Thể tích khối gỗ bằng:

A. 1539 $cm^{3}$

B. 945 $cm^{3}$

C. 270 $cm^{3}$

D. 513 $cm^{3}$

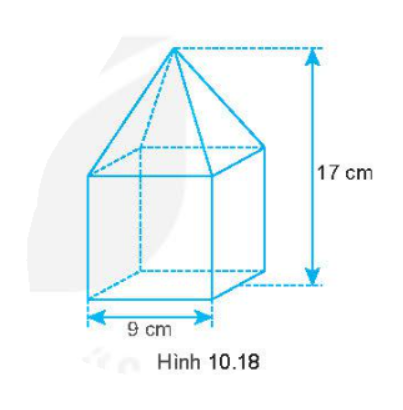
Đáp án: B

B. BÀI TẬP

Bài tập 10.16 toán 8 tập 2 KNTT trang 79: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 6 cm, chiều cao 8 cm như Hình 10.19. Tính thể tích hình chóp biết $\sqrt{27} \approx 5,2$.

Đáp án:

$\Delta$ ABC là tam giác đều nên CI là trung tuyến đồng thời là đường cao, ta có

BI = IA = $\frac{1}{2}AB$ = 3 (cm)

$\Delta$ ACI vuông tại I nên $IA^{2} + CI^{2} = AC^{2}$ (định lí Pythagore)

Hay $3^{2} + CI^{2} = 6^{2}$

do đó $CI^{2} = 36 – 9 = 27$

Vậy CI = $\sqrt{27} \approx 5,2$ (cm).

Diện tích $\Delta$ ABC là 

$S = \frac{1}{2} \cdot AB \cdot CI = \frac{1}{2} \cdot 6 \cdot 5,2 = 15,6$ ($cm^{2}$)

Thể tích của hình chóp tam giác đều S.ABC là

V = $\frac{1}{3} \cdot S \cdot h$ = $\frac{1}{3} \cdot 15,6 \cdot 8$ = 41,6 ($cm^{3}$)

Bài tập 10.17 toán 8 tập 2 KNTT trang 80: Cho hình chóp tam giác đều A.BCD có cạnh đáy bằng 12 cm, cạnh bên bằng 10 cm (H.10.20). Tính diện tích xung quanh của hình chóp.

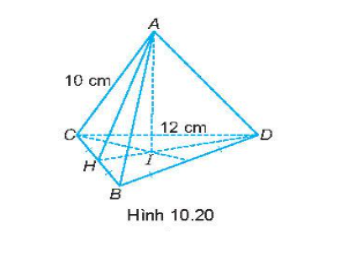
Đáp án:

Ta có CH = HB = 6 cm.

$\Delta$ ACH vuông tại H nên $AH^{2} + CH^{2} = AC^{2}$ (định lí Pythagore)

Hay $AH^{2} + 6^{2} = 10^{2}$

do đó $AH^{2} = 100 – 36 = 64$

Vậy AH = 8 (cm).

Diện tích xung quanh của hình chóp tam giác đều A.BCD là:

$S_{xq} = p \cdot d = \frac{12 \cdot 3}{2} \cdot 8 = 144$ ($cm^{2}$)

Bài tập 10.18 toán 8 tập 2 KNTT trang 80: Hình chóp tứ giác đều S.ABCD có thể tích bằng 144 cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, A (H.10.21). Tính thể tích của hình chóp S.MNPQ.

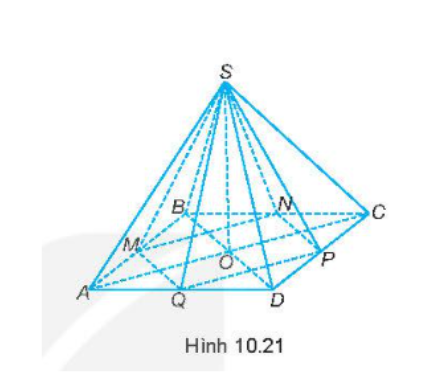
Đáp án:

MN là đường trung bình của tam giác ABC nên $MN = \frac{1}{2}AC$. Tương tự $MQ = \frac{1}{2}BD$.

Diện tích hình vuông MNPQ là

$S_{MNPQ} = MN \cdot MQ = \frac{1}{2}AC \cdot \frac{1}{2}BD = \frac{1}{2} (\frac{1}{2}AC \cdot BD) = \frac{1}{2}S_{ABCD}$

 Hai hình chóp S.MNPQ và S.ABCD có cùng chiều cao SO mà

$S_{MNPQ} = \frac{1}{2}S_{ABCD}$ 

nên $V_{S.MNPQ} = \frac{1}{2}V_{S.ABCD} = 72$ ($cm^{3}$)

Bài tập 10.19 toán 8 tập 2 KNTT trang 80: Một cái lều đồ chơi cho trẻ em có hình dạng gồm một hình lập phương có cạnh 1,2 m và nóc lều là một hình chóp tứ giác đều có cạnh đáy 1,2 m, trung đoạn bằng 0,8 m (H.10.22). Tính diện tích vải để phủ nóc và các mặt bên của lều (coi các mép nối không đáng kể)

Đáp án:

Diện tích tích các mặt bên của lều là $S_{1} = 4 \cdot 1,2^{2} =5,76$ ($m^{2}$).

Diện tích nóc lều là $S_{2} = 4 \cdot (\frac{1}{2} \cdot 1,2 \cdot 0,8) = 1,92$ ($m^{2}$).

Diện tích vải để phủ nóc và các mặt bên của lều là

$S =S_{1}+S_{2} = 5,76+1,92 = 7,68$ ($m^{2}$).

Bài tập 10.20 toán 8 tập 2 KNTT trang 80: Một khối đồ chơi làm bằng gỗ được tạo thành từ hai hình chóp tứ giác đều. Cạnh đáy của mỗi hình chóp tứ giác đều bằng 6 cm, trung đoạn của nó bằng 4 cm (H.10.23). Người ta sơn mặt ngoài của món đồ chơi. Hỏi diện tích cần sơn bằng bao nhiêu centimét vuông?

Đáp án:

Diện tích cần sơn là $S = 2 \cdot p \cdot d = (4 \cdot 6) \cdot 4 = 96$ ($cm^{2}$).