Bài tập 9.12 toán 8 tập 2 KNTT trang 55: Hai tam giác có độ dài ba cạnh như sau có đồng dạng không? Vì sao?

(1) 2 cm, 3 cm, 4 cm và 6 cm, 9 cm, 12 cm. 

(2) 3 cm, 5 cm, 6 cm và 6 cm, 10 cm, 11 cm.

(3) 2 cm, 3 cm, 3 cm và 2 cm, 2 cm, 3 cm.

(4) 4 cm, 4 cm, 4 cm và 3 cm, 3 cm, 3 cm.

Đáp án:

(1) Hai tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh vì 

$\frac{2}{6} = \frac{3}{9} = \frac{4}{12}$

(2) Hai tam giác không đồng dạng vì 

$\frac{3}{6} = \frac{5}{10} \neq \frac{6}{11}$

(3) Hai tam giác không đồng dạng vì 

$\frac{2}{2} \neq \frac{3}{2} \neq \frac{3}{3}$

(4) Hai tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh vì 

$\frac{4}{3} = \frac{4}{3} = \frac{4}{3}$

Bài tập 9.13 toán 8 tập 2 KNTT trang 55: Cho hai tam giác ABC và DEF lần lượt có chu vi là 15 cm và 20 cm. Biết rằng $\frac{AB}{DE} = \frac{AC}{DF} = \frac{3}{4}$. Chứng minh rằng $\triangle $ABC $\sim$ $\triangle $DEF.

Đáp án:

Từ giả thiết suy ra: $\frac{3}{4} = \frac{AB}{DE} = \frac{AC}{DF} = \frac{AB + AC}{DE+ DF} = \frac{15 - BC}{20 – EF}$

Do đó 60 – 3EF = 60 – 4BC hay $\frac{3}{4} = \frac{BC}{EF}$. 

Vậy hai tam giác ABC và DEF có 

$\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}$

Suy ra $\triangle $ABC $\sim$ $\triangle $DEF. 

Bài tập 9.14 toán 8 tập 2 KNTT trang 55: Cho hai tam giác ABC và MNP thoả mãn 2AB = 3AC = 4BC và DE = 6 cm, DF = 4 cm, EF = 3 cm. Chứng minh rằng $\triangle $ABC $\sim$ $\triangle $MNP.

Đáp án:

Từ giả thiết suy ra 2DE = 3DF = 4EF. Do đó hai tam giác ABC và DEF có 

$\frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF}$

Suy ra $\triangle $ABC $\sim$ $\triangle $DEF (c.c.c)

Bài tập 9.15 toán 8 tập 2 KNTT trang 55: Cho tam giác ABC và điểm O nằm trong tam giác. Lấy M, N, P là các điểm lần lượt trên các tia OA, OB, OC sao cho OA = 3OM, OB = 3ON, OC = 3OP. Chứng minh rằng$\triangle $ABC $\sim$ $\triangle $MNP và tìm tỉ số đồng dạng.

Đáp án:

Ta có: $\frac{OM}{OA} = \frac{ON}{OB} = \frac{1}{3}$ 

Do đó theo định lí Thales đảo áp dụng cho tam giác ABC và cát tuyến MN ta có: MN // AB. Vì vậy $\triangle $OMN $\sim$ $\triangle $OAB.

Suy ra $\frac{MN}{AB} = \frac{OM}{OA} = \frac{1}{3}$

Chứng minh tương tự có: 

$\frac{MP}{AC} = \frac{OM}{OA} = \frac{1}{3}$

$\frac{NP}{BC} = \frac{ON}{OB} = \frac{1}{3}$

Vì vậy, hai tam giác ABC và MNP có 

$\frac{AB}{MN} = \frac{AC}{MP} = \frac{BC}{NP} = 3$

Suy ra $\triangle $ABC $\sim$ $\triangle $MNP (c.c.c) với tỉ số đồng dạng bằng 3.

Bài tập 9.16 toán 8 tập 2 KNTT trang 55: Cho tam giác ABC và các điểm M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng $\triangle $ABC $\sim$ $\triangle $MNP và tìm tỉ số đồng dạng.

Đáp án:

Vì NP, PM, MN lần lượt là các đường trung bình ứng với các đỉnh A, B, C của tam giác ABC nên 

$\frac{NP}{BC} = \frac{PM}{CA} = \frac{MN}{AB} = \frac{1}{2}$

Suy ra $\triangle $MNP $\sim$ $\triangle $ABC với tỉ số đồng dạng bằng $\frac{1}{2}$

Bài tập 9.17 toán 8 tập 2 KNTT trang 55: Cho tứ giác ABCD với AB = 2 cm, AD= 3 cm, BD = 4 cm, BC = 6 cm, CD=8 cm. Chứng minh rằng $\triangle $ABC $\sim$ $\triangle $BDC và AB song song với CD.

Đáp án:

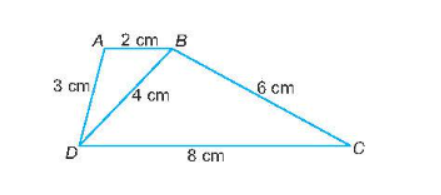
Hai tam giác ABD và BDC có 

$\frac{AB}{BD} = \frac{AD}{BC} = \frac{BD}{DC} = \frac{1}{2}$

Suy ra $\triangle $ABC $\sim$ $\triangle $BDC (c.c.c)

Suy ra $\widehat{ABD} = \widehat{BDC}$ (cặp góc tương ứng)

Vậy AB // DC do 2 góc so le trong bằng nhau.

Bài tập 9.18 toán 8 tập 2 KNTT trang 55: Cho tam giác ABC có độ dài các cạnh là AB = 4 cm, BC = 5 cm, CA = 6 cm. Tam giác MNP đồng dạng với tam giác ABC và có độ dài cạnh lớn nhất bằng 9 cm. Hãy cho biết độ dài các cạnh MN, MP, NP của tam giác MNP.

Đáp án:

Gọi k là tỉ số đồng dạng của tam giác MNP với tam giác ABC. Khi đó:

MN = kAB, NP = kBC, MP = kAC. Vì AB < BC < AC nên MN < NP < MP

Do vậy MP = 9 cm. Suy ra $k = \frac{MP}{AC} = \frac{3}{2}$

Suy ra $MN = \frac{3}{2}AB = 6 cm$

$NP = \frac{3}{2}BC = 7,5 cm$

Bài tập 9.19 toán 8 tập 2 KNTT trang 55: Với hai tam giác bất kì ABC và DEF thoả mãn $\frac{AB}{EF} = \frac{BC}{DF}$; $\widehat{ABC} = \widehat{DFE}$. Những khẳng định nào sau đây là đúng?

(1) $\triangle $ABC $\sim$ $\triangle $DEF.

(2)  $\triangle $CBA $\sim$ $\triangle $DEF.

(3) $\triangle $ABC $\sim$ $\triangle $EFD.

(4)  $\triangle $BCA $\sim$ $\triangle $EFD.

(5) $\triangle $ABC $\sim$ $\triangle $FDE.

(6) $\triangle $BAC$\sim$ $\triangle $FED.

Đáp án:

Hai tam giác ABC và DEF có 

$\frac{AB}{EF} = \frac{BC}{DF}$

$\widehat{ABC} = \widehat{DFE}$

Suy ra $\triangle $ABC $\sim$ $\triangle $EFD (c.g.c)

Do đó câu (2), (3) và (6) đúng; câu (1), (4) và (5) sai.

Bài tập 9.20 toán 8 tập 2 KNTT trang 56: Với hai tam giác bất kì ABC và MNP thoả mãn $\widehat{ABC} = \widehat{NMP}$, $\widehat{ACB} = \widehat{MNP}$. Những khẳng định nào sau đây là đúng?

(1) $\triangle $ABC $\sim$ $\triangle $MNP.

(2) $\triangle $BCA $\sim$ $\triangle $MNP.

(3) $\triangle $ABC $\sim$ $\triangle $NPM.

(4) $\triangle $CAB $\sim$ $\triangle $NPM.

(5) $\triangle $ABC $\sim$ $\triangle $PMN.

(6) $\triangle $BAC $\sim$ $\triangle $MNP.

Đáp án:

Hai tam giác ABC và MNP có 

$\widehat{ABC} = \widehat{NMP}$

$\widehat{ACB} = \widehat{MNP}$

Suy ra $\triangle $ABC $\sim$ $\triangle $PMN (g.g)

Do đó câu (2), (4) và (5) đúng; câu (1), (3) và (6) sai.

Bài tập 9.21 toán 8 tập 2 KNTT trang 56: Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho $AM \cdot AB = AN \cdot AC$

a) Chứng minh rằng $\triangle $AMN $\sim$ $\triangle $ACB.

b) Lấy E, F lần lượt là trung điểm của MN, BC. Chứng minh rằng $\widehat{EAB} = \widehat{FAC}$

Đáp án:

Từ $AM \cdot AB = AN \cdot AC$

Suy ra $\frac{AM}{AC} = \frac{AN}{AB}$

Hai tam giác AMN và ACB có 

$\frac{AM}{AC} = \frac{AN}{AB}$

$\widehat{MAN} = \widehat{BAC}$ (góc chung)

Suy ra $\triangle $AMN $\sim$ $\triangle $ACB (c.g.c)

b) Từ  $\triangle $AMN $\sim$ $\triangle $ACB suy ra 

$\widehat{AMN} = \widehat{ACB}$ 

$\frac{AM}{AC} = \frac{MN}{CB}$

Hai tam giác AME và ACF có 

$\frac{AM}{AC} = \frac{MN}{CB} = \frac{ME}{CF}$ (chứng minh trên)

$\widehat{AME} = \widehat{AMN} = \widehat{ACB}$ = \widehat{ACF}$ (chứng minh trên)

Suy ra $AME$\sim$ $\triangle $ACF (c.g.c)

Suy ra $\widehat{EAM} = \widehat{FAC}$. 

Vì $\widehat{EAB} = \widehat{EAM}$ nên $\widehat{EAB} = \widehat{FAC}$

Bài tập 9.22 toán 8 tập 2 KNTT trang 56: Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho $\widehat{APQ} = \widehat{ACB}$. Chứng minh rằng:

a) $AP \cdot AB = AQ \cdot AC$

b) $\widehat{APC} = \widehat{AQB}$

Đáp án:

a) Hai tam giác ACB và APQ có 

$\widehat{BAC} = \widehat{QAP}$ (2 góc đối đỉnh)

$\widehat{ACB} = \widehat{APQ}$ (giả thiết)

Suy ra $\triangle $ACB $\sim$ $\triangle $APQ (g.g)

Suy ra $\frac{AB}{AQ} = \frac{AC}{AP}$ hay $AP \cdot AB = AQ \cdot AC$

b) Từ $AP \cdot AB = AQ \cdot AC$

Suy ra $\frac{AP}{AQ} = \frac{AC}{AB}$

Hai tam giác APC và AQB có 

$\frac{AP}{AQ} = \frac{AC}{AB}$ (chứng minh trên)

$\widehat{PAC} = \widehat{QAB}$ (2 góc đối đỉnh)

Suy ra $\triangle $APC $\sim$ $\triangle $AQB (c.g.c)

Bài tập 9.23 toán 8 tập 2 KNTT trang 56: Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và ABC. Chứng minh rằng:

a) $\triangle $MEN $\sim$ $\triangle $BFC

b) $\frac{AE}{AF} = \frac{MN}{BC}$

Đáp án:

Vì ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và ABC

Suy ra $\widehat{NME} = \frac{\widehat{AMN}}{2}$

$\widehat{CBF} = \frac{\widehat{ABC}}{2}$

Vì MN // BC nên $\widehat{AMN} = \widehat{ABC}$ (2 góc đồng vị)

Từ đó suy ra $\widehat{NME} = \frac{\widehat{AMN}}{2} = \frac{\widehat{ABC}}{2} = \widehat{CBF}$

Hai tam giác MEN và BFC có 

$\widehat{MNE} = \widehat{BCF}$ (2 góc đồng vị, MN // BC)

$\widehat{NME} = \widehat{CBF}$ (chứng minh trên)

Suy ra $\triangle $MEN $\sim$ $\triangle $BFC (g.g)

b) $\widehat{AME} = \frac{\widehat{AMN}}{2} = \frac{\widehat{ABC}}{2} = \widehat{ABF}$

Suy ra ME // BF (2 góc đồng vị bằng nhau)

Áp dụng định lí Thales, ta được: $\frac{AE}{AF} = \frac{AM}{AB}$

Mặt khác MN // BC nên $\triangle $AMN $\sim$ $\triangle $ABC 

Suy ra $\frac{AM}{AB} = \frac{MN}{BC}$

Vậy $\frac{AE}{AF} = \frac{AM}{AB} = \frac{MN}{BC}$

Bài tập 9.24 toán 8 tập 2 KNTT trang 56: Cho hình thang ABCD (AB // CD). Biết rằng AB = 2 cm, BD = 4 cm, CD = 8 cm. Chứng minh rằng BC = 2AD.

Đáp án:

Hai tam giác ABD và BDC có 

$\frac{AB}{BD} = \frac{BD}{DC} =  \frac{1}{2}$

$\widehat{ABD} = \widehat{BDC}$ (2 góc so le trong, AB // CD)

Suy ra $\triangle $MABD $\sim$ $\triangle $BCD (c.g.c)

Suy ra $\frac{AD}{BC} = \frac{AB}{BD} =  \frac{1}{2}$

Vậy BC = 2AD

Bài tập 9.25 toán 8 tập 2 KNTT trang 56: Cho hình thang ABCD (AB // CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F. 

a) Chứng minh rằng: $\triangle $EAB$\sim$ $\triangle $EDC, $\triangle $FAB$\sim$ $\triangle $FCD

b) Lấy hai điểm M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, E, F thẳng hàng.

Đáp án:

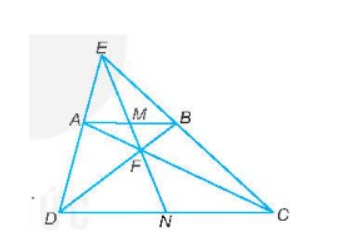
a) Vì AB // DC (tam giác EDC) nên $\triangle $EAB$\sim$ $\triangle $ED

AB // CD (tam giác FDC) nên $\triangle $FAB$\sim$ $\triangle $FCD

b) Từ $\triangle $EAB$\sim$ $\triangle $EDC suy ra 

$\frac{EA}{ED} = \frac{AB}{DC} = \frac{AM}{DN}$

Hai tam giác EAM và EDN có 

$\frac{AB}{BD} = \frac{BD}{DC}$ (cmt)

$\widehat{EAM} = \widehat{EDN}$ (2 góc đồng vị, AM // DN)

Suy ra $\triangle $EAM$\sim$ $\triangle $EDN (c.g.c)

Suy ra $\widehat{AEM} = \widehat{DEN}$

Vậy tia EM trùng với tia EN hay E, M, N thẳng hàng. 

Từ  $\triangle $FAB$\sim$ $\triangle $FCD suy ra 

$\frac{FA}{FC} = \frac{AB}{CD} = \frac{AM}{CN}$

Hai tam giác FAM và FCN có 

$\frac{FA}{FC} = \frac{AM}{CN}$ (cmt)

$\widehat{FAM} = \widehat{FCN}$ (2 góc so le trong, AM // CN)

Suy ra  $\triangle $FAM$\sim$ $\triangle $FCN (c.g.c)

Suy ra $\widehat{AFM} = \widehat{CFN}$

Vậy tia FM và FN là 2 tia đối nhau, hay F, M, N thẳng hàng. 

Do đó 4 điểm M, N, E, F thẳng hàng.

Bài tập 9.26 toán 8 tập 2 KNTT trang 56: Cho tam giác ABC với AB = 6 cm, AC = 9 cm. Lấy điểm D trên cạnh AC sao cho AD = 4 cm. Chứng minh rằng $\triangle $ABD$\sim$ $\triangle $ACB và $BC = \frac{3}{2}BD$.

Đáp án:

Hai tam giác ABD và ACB có 

$\frac{AB}{AC} = \frac{AD}{AB} =  \frac{2}{3}$

$\widehat{BAD} = \widehat{CAB}$ (góc chung)

Suy ra $\triangle $ABD$\sim$ $\triangle $ACB (c.g.c)

Suy ra $\frac{BD}{BC} = \frac{AB}{AC} =  \frac{2}{3}$

Vậy $BC = \frac{3}{2}BD$

Bài tập 9.27 toán 8 tập 2 KNTT trang 57: Cho tứ giác ABCD như Hình 9.6. Biết rằng AB = 2 cm, AC = 4 cm, AD = 8 cm và AC là phân giác của góc BAD. Chứng minh rằng CD = 2BC.

Đáp án:

Hai tam giác ACD và ABC có 

$\frac{AC}{AB} = \frac{AD}{AC} = 2$

$\widehat{DAC} = \widehat{CAB}$ (giả thiết)

Suy ra $\triangle $ACD$\sim$ $\triangle $ABC (c.g.c)

Suy ra $\frac{CD}{BC} = \frac{AC}{AB} = 2$

Vậy CD = 2BC.

Bài tập 9.28 toán 8 tập 2 KNTT trang 57: Cho tam giác ABC và điểm D trên cạnh AC sao cho $\widehat{ABD} = \widehat{BCA}$. Chứng minh rằng $AB^{2} = AD \cdot AC$

Đáp án:

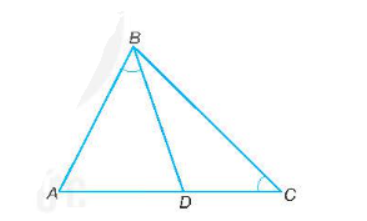
Hai tam giác ABD và ACB có 

$\widehat{A}$ chung

$\widehat{ABD} = \widehat{ACB}$

Suy ra $\triangle $ABD$\sim$ $\triangle $ACB (g.g)

Suy ra $\frac{AB}{AC} = \frac{AD}{AB}$ hay $AB^{2} = AD \cdot AC$

Bài tập 9.29 toán 8 tập 2 KNTT trang 57: Cho hai điểm M, N lần lượt nằm trên các cạnh AB, AC của tam giác ABC sao cho $\widehat{ABN} = \widehat{ACM}$. Gọi O là giao điểm của BN và CM. Chứng minh rằng:

a) $AM \cdot AB = AN \cdot AC$

b) $OM \cdot OC = ON \cdot OB$

Đáp án:

a) Hai tam giác ABN và ACM có 

$\widehat{A}$ chung

$\widehat{ABN} = \widehat{ACM}$ (giả thiết)

Suy ra $\triangle $ABN$\sim$ $\triangle $ACM (g.g)

Suy ra $\frac{AB}{AC} = \frac{AN}{AM}$ hay $AM \cdot AB = AN \cdot AC$

b) Hai tam giác OBM và OCN có 

$\widehat{MOB} = \widehat{NOC}$ (2 góc đối đỉnh)

$\widehat{MBO} = \widehat{ABN}= \widehat{ACM} = \widehat{NCO}$ (giả thiết)

Suy ra $\triangle $OBM$\sim$ $\triangle $OCN (g.g)

Suy ra $\frac{OM}{ON} = \frac{OB}{OC}$ hay $OM \cdot OC = ON \cdot OB$

Bài tập 9.30 toán 8 tập 2 KNTT trang 57: Cho tam giác ABC với AB = 6 cm, AC = 4 cm, BC = 5 cm. Trên tia đối của tia CA, lấy điểm D sao cho CD=CB. Chứng minh rằng:

a) $\triangle $ABC $\sim$ $\triangle $ADB.

b) $\widehat{ACB} = 2\widehat{ABC}$

Đáp án:

a) Hai tam giác ABC và ADB có 

$\frac{AB}{AD} = \frac{AB}{AC+DC} = \frac{AB}{AC+BC} = \frac{2}{3} = \frac{AC}{AB}$

$\widehat{A}$ chung

Suy ra $\triangle $ABC $\sim$ $\triangle $ADB (c.g.c)

b) Do tam giác CBD cân (CD=CB) suy ra 

$\widehat{ACB} = 2\widehat{CDB} = 2\widehat{ADB}$ (tính chất góc ngoài tam giác cân)

Mặt khác $\widehat{ADB} = \widehat{ABC}$ ($\triangle $ABC $\sim$ $\triangle $ADB)

Suy ra $\widehat{ACB} = 2\widehat{ABC}$