Bài tập 9.42 toán 8 tập 2 KNTT trang 62: 

(1) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia.

(2) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia.

(3) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.

(4) Một góc nhọn của tam giác này phụ với một góc nhọn của tam giác kia.

(5) Cạnh huyền của tam giác này bằng cạnh huyền của tam giác kia.

(6) Một cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với một cạnh góc vuông và cạnh huyền của tam giác kia.

Đáp án:

Những điều kiện (1), (3), (4), (6) kéo theo hai tam giác vuông đồng dạng.

Bài tập 9.43 toán 8 tập 2 KNTT trang 62: Cho tam giác ABC vuông cân tại A và tam giác MNP CÓ MN = MP = 4 cm và NP = $4\sqrt{2}$ cm. Chứng minh rằng $\triangle $ABC $\sim$ $\triangle $MNP.

Đáp án:

Do $MN^{2} + MP^{2} = NP^{2}$ nên tam giác MNP vuông cân tại đỉnh M (theo định lí Pythagore đảo)

Hai tam giác vuông cân ABC (vuông tại A) và MNP (vuông tại M) có 

$\frac{AB}{MN} = \frac{AC}{MP}$

Suy ra $\triangle $ABC $\sim$ $\triangle $MNP (cạnh góc vuông – cạnh góc vuông)

Bài tập 9.44 toán 8 tập 2 KNTT trang 63: Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng?

Đáp án:

$\triangle $ABC $\sim$ $\triangle $MPN (cạnh góc vuông – cạnh góc vuông)

$\triangle $MNP $\sim$ $\triangle $EDF (một cặp góc nhọn bằng nhau)

$\triangle $ABC $\sim$ $\triangle $GHK (cạnh góc vuông – cạnh huyền)

Bài tập 9.45 toán 8 tập 2 KNTT trang 63: Cho tam giác ABC vuông tại A có đường cao AH. Từ H kẻ đường thẳng HE vuông góc với AB (E thuộc AB ). Chứng minh rằng:

a) $\triangle $ABC $\sim$ $\triangle $HAC và $CA^{2} = CH \cdot CB$

b) $\frac{AH}{BC} = \frac{HE}{AB}$

Đáp án:

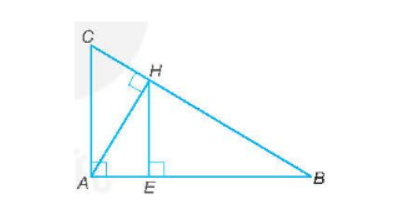
a) Hai tam giác vuông ABC (vuông tại A) và HAC (vuông tại H) có 

$\widehat{C}$ chung

Suy ra $\triangle $ABC $\sim$ $\triangle $HAC (một cặp góc nhọn bằng nhau)

Suy ra $\frac{CA}{CH} = \frac{CB}{CA}$ hay $CA^{2} = CH \cdot CB$

b) Hai tam giác vuông ABC (vuông tại A) và EHA (vuông tại E) có 

$\widehat{ACB} = 90^{o} - \widehat{ABC} = 90^{o} - \widehat{ABH} = \widehat{HAB} = \widehat{HAE}$

Suy ra $\triangle $ABC $\sim$ $\triangle $EHA (một cặp góc nhọn bằng nhau)

Suy ra $\frac{AB}{EH} = \frac{BC}{HA}$ hay $\frac{AH}{BC} = \frac{HE}{AB}$

Bài tập 9.46 toán 8 tập 2 KNTT trang 63: Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng AB = 6 cm và AC = 8 cm, hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.

Đáp án:

Áp dụng đính lí Pythagore cho tam giác ABC vuông tại A, ta có

$BC^{2} = AB^{2} + AC^{2} = 6^{2} + 8^{2} = 100$

Suy ra BC = 10 cm.

Mặt khác $\frac{BC \cdot AH}{2} = \frac{AB \cdot AC}{2}$ (diện tích tam giác ABC)

Suy ra AH = $\frac{AB \cdot AC}{BC}$ = 4,8 cm

Hai tam giác vuông ABC (vuông tại A) và HBA (vuông tại H) có 

$\widehat{B}$ chung

Suy ra $\triangle $ABC $\sim$ $\triangle $HBA

Suy ra $\frac{AB}{HB} = \frac{BC}{BA}$ hay 

BH = $\frac{AB^{2}}{BC}$ = 3,6 cm

Tương tự: CH = $\frac{AC^{2}}{BC}$ = 6,4 cm

Bài tập 9.47 toán 8 tập 2 KNTT trang 63: Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:

a) $HA \cdot HD = HB \cdot HE = HC \cdot HF$

b) $\triangle $AFC $\sim$ $\triangle $AEB và $AF \cdot AB = AE \cdot AC$

c) $\triangle $BDF $\sim$ $\triangle $EDC và DA là tia phân giác của góc EDF.

Đáp án:

a) Hai tam giác vuông HAE (vuông tại E) và HBD (vuông tại D) có 

$\widehat{AHE} = \widehat{DHB}$ (2 góc đối đỉnh)

Suy ra $\triangle $HAE $\sim$ $\triangle $HBD (một cặp góc nhọn bằng nhau)

Suy ra $\frac{HA}{HB} = \frac{HE}{HD}$ hay $HA \cdot HD = HB \cdot HE$

Tương tự: $HA \cdot HD = HC \cdot HF$

Suy ra $HA \cdot HD = HB \cdot HE = HC \cdot HF$

b) Hai tam giác vuông AFC (vuông tại F) và AEB (vuông tại E) có 

$\widehat{A}$ chung

Suy ra $\triangle $AFC $\sim$ $\triangle $AEB (một cặp góc nhọn bằng nhau)

Suy ra $\frac{AF}{AE} = \frac{AC}{AB}$ hay $AF \cdot AB = AE \cdot AC$

c) Từ $HA \cdot HD = HB \cdot HE$

Suy ra $\frac{HA}{HE} = \frac{HB}{HD}$

Hai tam giác AHB và EHD có 

$\widehat{AHB} = \widehat{EHD}$ (2 góc đối đỉnh)

$\frac{HA}{HE} = \frac{HB}{HD}$

Suy ra $\triangle $AHB $\sim$ $\triangle $EHD

Suy ra $\widehat{HAB} = \widehat{HED}$

Suy ra $\widehat{CED} = 90^{o} - \widehat{HED} = 90^{o} - \widehat{HEB} = \widehat{FBD}$

Tương tự ta có $\widehat{BFD} = \widehat{ECD}$

Hai tam giác BDF và EDC có 

$\widehat{FBD} = \widehat{CED}$ 

$\widehat{BFD} = \widehat{ECD}$ 

Suy ra $\triangle $BDF $\sim$ $\triangle $EDC (g.g)

Suy ra $\widehat{FDB} = \widehat{CDE}$

Suy ra $\widehat{FDA}= 90^{o} - \widehat{FDB} = 90^{o} - \widehat{CDE} = \widehat{EDA}$ 

Suy ra DA là tia phân giác của góc EDF.

Bài tập 9.48 toán 8 tập 2 KNTT trang 63: Cho tam giác nhọn ABC có các đường cao AD, BE, CF. Chứng minh rằng:

a) $\triangle $BDF $\sim$ $\triangle $BAC và $\triangle $CDE $\sim$ $\triangle $CAB

b) $BF \cdot BA + CE \cdot CA = BC^{2}$

Đáp án:

Hai tam giác vuông BDA (vuông tại D) và BFC (vuông tại F) có 

$\widehat{B}$ chung

Suy ra $\triangle $BDA $\sim$ $\triangle $BFC  (một cặp góc nhọn bằng nhau)

Suy ra $\frac{BD}{BF} = \frac{BA}{BC}$ 

hay $\frac{BF}{BC} = \frac{BD}{BA}$ 

Hai tam giác BDF và BAC có 

$\frac{BF}{BC} = \frac{BD}{BA}$  (chứng minh trên)

$\widehat{B}$ chung

Suy ra $\triangle $BDF $\sim$ $\triangle $BAC (c.g.c)

Tương tự: $\triangle $CDE $\sim$ $\triangle $CAB

b) $\triangle $BDF $\sim$ $\triangle $BAC

Suy ra $\frac{BF}{BC} = \frac{BD}{BA}$ hay $BF \cdot BA = BD \cdot BC$

$\triangle $CDE$\sim$ $\triangle $CAB

Suy ra $\frac{CE}{CB} = \frac{CD}{CA}$ hay $CE \cdot CA = CD \cdot BC$

Vậy $BF \cdot BA + CE \cdot CA = BD \cdot BC + CD \cdot BC = BC^{2}$

Bài tập 9.49 toán 8 tập 2 KNTT trang 63: Cho tam giác ABC vuông tại A có đường cao AH. Cho M là một điểm nằm trên cạnh BC (M nằm giữa C và H). Kẻ đường thẳng qua M vuông góc với BC lần lượt cắt AC và tia đối của tia AB tại N và P. Chứng minh rằng:

$\triangle$ ANP $\sim$ $\triangle$ HBA và $\triangle$ MCN $\sim$ $\triangle$ MPB

b) $\frac{MB}{MC} \cdot \frac{NC}{NA} \cdot \frac{PA}{PB} = 1$

Đáp án:

a) Hai tam giác vuông ANP (vuông tại A) và HBA (vuông tại H) có 

$\widehat{ANP} = \widehat{MNC} = 90^{o} - \widehat{NCM} = 90^{o} - \widehat{ACB} = \widehat{CBA} = \widehat{HBA}$

Suy ra $\triangle$ ANP $\sim$ $\triangle$ HBA (một cặp góc nhọn bằng nhau)

Hai tam giác vuông MCN (vuông tại M) và MPB (vuông tại M) có 

$\widehat{MNC} = 90^{o} - \widehat{MCN} = 90^{o} - \widehat{BCA} = \widehat{CBA} = \widehat{MBP}$

Suy ra $\triangle$ MCN $\sim$ $\triangle$ MPB (một cặp góc nhọn bằng nhau)

b) Áp dụng định lí Thalès cho MN // AH và AH // MP, ta được:

$\frac{MB}{MC} \cdot \frac{NC}{NA} \cdot \frac{PA}{PB}$ 

= $\frac{MB}{PB} \cdot \frac{NC}{NA} \cdot \frac{PA}{MC}$

= $\frac{MH}{PA} = \frac{MC}{MH} = \frac{PA}{MC}$

= 1

Bài tập 9.50 toán 8 tập 2 KNTT trang 64: Cho tứ giác ABCD như Hình 9.11. Biết rằng $\widehat{BAD} = \widehat{BDC} = 90^{o}$, AD = 4cm, BD=6 cm và BC=9 cm. Chứng minh rằng BC // AD.

Đáp án:

Hai tam giác vuông ABD (vuông tại A) và DCB (vuông tại D) có 

$\frac{AD}{DB} = \frac{DB}{BC} = \frac{2}{3}$

Suy ra $\triangle$ ABD $\sim$ $\triangle$ DCB (cạnh góc vuông – cạnh huyền)

Suy ra $\widehat{ADB} = \widehat{DBC}$

Suy ra AD // BC (cặp góc so le trong bằng nhau)

Bài tập 9.51 toán 8 tập 2 KNTT trang 64: Cho tam giác ABC vuông tại A có đường cao AHGọi M, N lần lượt là chân đường vuông góc kẻ từ H xuống AB và AC. Chứng minh rằng:

a) $AM \cdot AB = AH^{2}$ và $AM \cdot AB = AN \cdot AC$

b) $\triangle$ AMN $\sim$ $\triangle$ ACB

Đáp án:

a) Hai tam giác vuông AHM (vuông tại M) và ABH (vuông tại H) có 

$\widehat{A}$ chung

Suy ra $\triangle$ AHM $\sim$ $\triangle$ ABH (một cặp góc nhọn bằng nhau)

Suy ra $\frac{AM}{AH} = \frac{AH}{AB}$ hay $AM \cdot AB = AH^{2}$

Tương tự: $AN \cdot AC = AH^{2}$

Suy ra $AM \cdot AB = AN \cdot AC$

b) Từ $AM \cdot AB = AN \cdot AC$

Suy ra $\frac{AM}{AC} = \frac{AN}{AB}$

Hai tam giác AMN và ACB có 

$\widehat{A}$ chung

$\frac{AM}{AC} = \frac{AN}{AB}$

Suy ra $\triangle$ AMN $\sim$ $\triangle$ ACB (c.g.c)

Bài tập 9.52 toán 8 tập 2 KNTT trang 64: Cho ABC và A'B'C' lần lượt là các tam giác vuông tại đỉnh A và A'. Gọi M, M' lần lượt là trung điểm của AC và A'C'. Chứng minh rằng:

a) $BC^{2} + 3BA^{2} = 4BM^{2}$ và $B’C’^{2} + 3B’A’^{2} = 4B’M’^{2}$

b) Nếu $\frac{BC}{BM} = \frac{B’C’}{B’M’}$ thì $\triangle$ ABC $\sim$ $\triangle$ A’B’C’

Đáp án:

a) Áp dụng đính lí Pythagore cho tam giác ABC vuông tại A, ta có

$4BM^{2} = 4(BA^{2} + AM^{2}) = 4BA^{2} + AC^{2} = 3BA^{2} + BC^{2}$

Tương tự: 

$4B’M’^{2} = 4(B’A’^{2} + A’M’^{2}) = 4B’A’^{2} + A’C’^{2} = 3B’A’^{2} + B’C’^{2}$

b) Giả sử $\frac{BC}{BM} = \frac{B’C’}{B’M’}$. Theo phần trên ta có:

$\frac{BC^{2}}{BM^{2}} + 3\frac{BA^{2}}{BM^{2}}$

= 4

= $\frac{B’C’^{2}}{B’M’^{2}} + 3\frac{B’A’^{2}}{B’M’^{2}}$

Suy ra $\frac{BA^{2}}{BM^{2}}$ = $\frac{B’A’^{2}}{B’M’^{2}}$

Hay $\frac{BA}{BM} = \frac{B’A’}{B’M’}$

Vậy $\frac{BC}{B’C’} = \frac{BM}{B’M’} = \frac{BA}{B’A’}$

Hai tam giác vuông ABC (vuông tại A) và A’B’C’ (vuông tại A’) có 

$\frac{BC}{B’C’} = \frac{BA}{B’A’}$

Suy ra $\triangle$ ABC $\sim$ $\triangle$ A’B’C’ (cạnh góc vuông – cạnh huyền)

Bài tập 9.53 toán 8 tập 2 KNTT trang 64: Cho hình vuông ABCD và M, N lần lượt là trung điểm của AB, BC. Gọi O là giao điểm của CM và DN

a) Chứng minh rằng CM $\bot$ DN.

b) Biết AB = 4 cm, hãy tính diện tích tam giác ONC.

Đáp án:

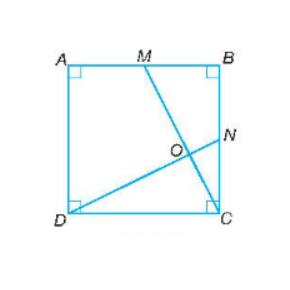
a) Dễ thấy tam giác CBM = tam giác DCN (hai tam giác vuông có hai cặp cạnh góc vuông tương ứng bằng nhau). 

Do đó $\widehat{CNO} + \widehat{NCO}$

= $\widehat{CND} + \widehat{BCM}$

= $\widehat{BMC} + \widehat{BCM}$

= $90^{o}$

Vì tổng các góc trong tam giác CNO bằng $180^{o}$

Nên $\widehat{NOC} = 180^{o} - \widehat{CNO} - \widehat{NCO} = 90^{o}$

Suy ra $CM \bot DN$

b) Áp dụng định lí Pythagore cho tam giác CND vuông tại C, ta được: 

$ND^{2} = NC^{2} + CD^{2} = 5NC^{2}$

$\frac{NC}{ND} = \frac{1}{\sqrt{5}}$

Hai tam giác vuông ONC (vuông tại O) và CND (vuông tại C) có 

$\widehat{N}$ (góc chung). 

Suy ra $\triangle$ ONC $\sim$ $\triangle$ CND (một cặp góc nhọn bằng nhau).

Do đó:

$\frac{ON}{CN} = \frac{OC}{CD} = \frac{NC}{ND} = \frac{1}{\sqrt{5}}$

Vậy diện tích tam giác ONC là:

$\frac{ON \cdot OC}{2} = \frac{1}{5} \cdot \frac{CN \cdot CD}{2}$

 = 0,8 ($cm^{2}$).