Bài tập 7.33 toán 8 tập 2 KNTT trang 33: Tìm hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1; 2) và có hệ số góc là –3.

Đáp án:

Giả sử hàm số bậc nhất cần tìm là y = ax + b (a $\neq$ 0 ). 

Đồ thị của hàm số này là một đường thẳng.

Hệ số góc của đường thẳng này là –3 nên a = –3. 

Đường thẳng này đi qua điểm (1; 2) nên suy ra 2 = $–3 \cdot 1+ b$ hay b = 5.

Vậy hàm số bậc nhất cần tìm là y = −3x + 5.

Bài tập 7.34 toán 8 tập 2 KNTT trang 33: Tìm hàm số bậc nhất có đồ thị là đường thẳng với hệ số góc là 2 và cắt trục hoành tại điểm có hoành độ bằng –3.

Đáp án:

Giả sử hàm số bậc nhất cần tìm là y = ax + b (a $\neq$ 0 ). 

Đồ thị của hàm số này là một đường thẳng.

Hệ số góc của đường thẳng này là 2 nên a = 2 

Đường thẳng này cắt trục hoành tại điểm có hoành độ bằng –3 nên suy ra 

0 = $2 \cdot (–3)+ b$ hay b = 6

Vậy hàm số bậc nhất cần tìm là y = 2x + 6.

Bài tập 7.35 toán 8 tập 2 KNTT trang 33: Hãy chỉ ra các cặp đường thẳng song song và các cặp đường thẳng cắt nhau trong các đường thẳng sau:

a) y = 2x + 1

b) y = –3x + 1

c) y = –3x + 2

d) y = 2x + 2.

Đáp án:

Các cặp đường thẳng song song là: 

y = 2x + 1 và y = 2x + 2 (vì có cùng hệ số góc là 2);

y = −3x + 1 và y = −3x + 2 (vì có cùng hệ số góc là −3)

Các cặp đường thẳng cắt nhau là: 

y = 2x + 1 và y = −3x + 1; 

y = 2x + 1 và y = −3x + 2;

y = 2x + 2 và y = −3x + 1; 

y = 2x + 2 và y = −3x + 2.

Bài tập 7.36 toán 8 tập 2 KNTT trang 33: Cho hai hàm số y = 2x + 3m và y = (2m + 1)x – 5. Tìm các giá trị của m để đồ thị của hai hàm số là:

a) Hai đường thẳng song song

b) Hai đường thẳng cắt nhau.

Đáp án:

a) Hai đường thẳng song song khi 2 = 2m + 1 hay m = $\frac{1}{2}$ và $3m \neq –5$ hay $m \neq \frac{-5}{3}$ 

Vậy m = $\frac{1}{2}$

b) Hai đường thẳng cắt nhau khi $2 \neq 2m+1$ hay $m \neq \frac{1}{2}$

Bài tập 7.37 toán 8 tập 2 KNTT trang 33: Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng y = −2x + 1 và đi qua điểm (−1; 4).

Đáp án:

Giả sử đường thẳng (d) y = ax + b (a $\neq$ 0) song song với đường thẳng y = −2x + 1, suy ra a = −2. 

Do (d) đi qua điểm (−1; 4) nên 4 = $−2 \cdot (−1)+b$ hay b = 2. Vậy hàm số cần tìm là y = –2x+2.

Bài tập 7.38 toán 8 tập 2 KNTT trang 34: Người ta chứng minh được rằng hai đường thẳng y = ax + b (a $\neq$ 0) và y = a’x + b’ (a’ $\neq$ 0) vuông góc với nhau khi tích hai hệ số góc của chúng bằng −1 tức là khi aa’ =-1. Tìm giá trị của m để đường thẳng y=(2m-4)x + 3 (m $\neq$ 2) vuông góc với đường thẳng y = $ \frac{-1}{2}x+1$

Đáp án:

Ta có aa’= –1 suy ra $(2m–4) \cdot \frac{–1}{2}$ = –1 hay m = 3.

Bài tập 7.39 toán 8 tập 2 KNTT trang 34: Trên cùng mặt phẳng toạ độ Oxy, cho hai đường thẳng ($d_{m}$): y=(1−m)x+2 và ($d’_{m}$): y=(m+1)x−3. Tuỳ theo giá trị của m xét vị trí tương đối giữa hai đường thẳng đã cho.

Đáp án:

Nếu 1 – m =m+1 hay m = 0 thì hai đường thẳng đã cho song song với nhau.

Nếu 1 – m $\neq$ m+1 hay m $\neq$ 0 thì hai đường thẳng đã cho cắt nhau.

Bài tập 7.40 toán 8 tập 2 KNTT trang 34: Inch (viết tắt là in) là một đơn vị chiều dài trong hệ đo lường Mỹ Phần đường thẳng trong hình vẽ sau mô tả sự quy đổi từ x (in) sang y (cm).

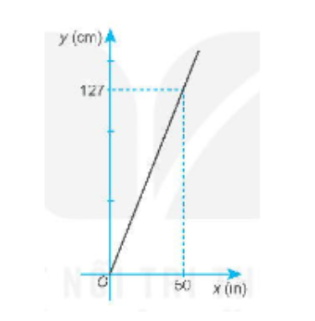
a) Tính hệ số góc của đường thẳng này

b) Đại lượng y có tỉ lệ thuận với đại lượng x không? Nếu có thì hệ số tỉ lệ bằng bao nhiêu?

c) Đại lượng x có tỉ lệ thuận với đại lượng y không? Nếu có thì hệ số tỉ lệ bằng bao nhiêu?

Đáp án:

a) Đường thẳng đi qua gốc toạ độ (và không trùng với hai trục toạ độ) nên nó là đồ thị của một hàm số bậc nhất có dạng y = ax (a $\neq$ 0).

Vì điểm (50; 127) thuộc đồ thị nên ta có 127 = $a \cdot 50$

Suy ra a = $\frac{127}{50}$ = 2,54. 

Vậy hệ số góc của đường thẳng là 2,54.

b) Vì y=2,54x nên đại lượng y tỉ lệ thuận với đại lượng x và hệ số tỉ lệ bằng 2,54.

c) Ta có x = ($1 \div 2,54$)y = $\frac{50}{127}y$ nên đại lượng x cũng tỉ lệ thuận với đại lượng y và hệ số tỉ lệ bằng $\frac{50}{127}$.