Bài tập 6.15 toán 8 tập 2 KNTT trang 9: Tính các tổng sau: 

a) $\frac{x^{2} - 2}{x(x-1)^{2}}$ + $\frac{2 - x}{x(x-1)^{2}}$ 

b) $\frac{1 - 2x}{6x^{3}y}$ + $\frac{3+2x}{6x^{3}y}$ + $\frac{2x-4}{6x^{3}y}$

Đáp án: 

a) $\frac{x^{2} - 2}{x(x-1)^{2}} + \frac{2 - x}{x(x-1)^{2}}$ 

= $\frac{x^{2} - 2 + 2 - x}{x(x-1)^{2}}$ 

= $\frac{x^{2} - x}{x(x-1)^{2}}$ 

= $\frac{x(x-1)}{x(x-1)^{2}}$ 

= $\frac{1}{x-1}$

b) $\frac{1 - 2x}{6x^{3}y} + \frac{3+2x}{6x^{3}y} + \frac{2x-4}{6x^{3}y}$

= $\frac{2x}{6x^{3}y}$ 

= $\frac{1}{3x^{2}y}$

Bài tập 6.16 toán 8 tập 2 KNTT trang 9: Tính các hiệu sau: 

a) $\frac{2x^{2}-1}{x^{2}-3x}$ - $\frac{(x+1)(x-1)}{x^{2}-3x}$

b) $\frac{1}{2x-3}$ - $\frac{13}{(2x-3)(4x+7)}$ 

Đáp án:

a) $\frac{2x^{2}-1}{x^{2}-3x}$ - $\frac{(x+1)(x-1)}{x^{2}-3x}$ 

= $\frac{2x^{2} - 1 - (x^{2} -1)}{x^{2}-3x}$ 

= $\frac{x^{2}}{x^{2}-3x}$ 

= $\frac{x}{x-3}$

b) $\frac{1}{2x-3}$ - $\frac{13}{(2x-3)(4x+7)}$ 

= $\frac{(4x+7)-13}{(2x-3)(4x+7)}$ 

= $\frac{4x-6}{(2x-3)(4x+7)}$ 

= $\frac{2}{4x+7}$

Bài tập 6.17 toán 8 tập 2 KNTT trang 9: Tính: 

a) $\frac{5x+y^{2}}{x^{2}y}$ - $\frac{5y-x^{2}}{xy^{2}}$ 

b) $\frac{y}{2x^{2}-xy}+\frac{4x}{y^{2}-2xy}$ 

Đáp án: 

a) $\frac{5x+y^{2}}{x^{2}y}$ - $\frac{5y-x^{2}}{xy^{2}}$ 

= $\frac{5xy+y^{3}-5xy+x^{3}}{x^{2}y^{2}}$ 

= $\frac{x^{3}+y^{3}}{x^{2}y^{2}}$

b) $\frac{y}{2x^{2}-xy}+\frac{4x}{y^{2}-2xy}$ 

= $\frac{y^{2}}{xy(2x-y)} + \frac{4x(-x)}{xy(2x-y)}$ 

= $\frac{-4x^{2}+y^{2}}{xy(2x-y)}$ 

= $\frac{(y-2x)(y+2x)}{xy(2x-y)}$ 

= $\frac{-2x -y}{xy}$

Bài tập 6.18 toán 8 tập 2 KNTT trang 9: Tính các tổng sau: 

a) $\frac{5}{6x^{2}y}$ + $\frac{7}{12xy^{2}}$ + $\frac{11}{18xy}$ 

b) $\frac{x^{3}+2x}{x^{3}+1}$ + $\frac{2x}{x^{2}-x+1}$ + $\frac{1}{x+1}$

Đáp án: 

a) $\frac{5}{6x^{2}y}$ + $\frac{7}{12xy^{2}}$ + $\frac{11}{18xy}$ 

= $\frac{30y}{36x^{2}y^{2}}$ + $\frac{21x}{36x^{2}y^{2}}$ + $\frac{22xy}{36x^{2}y^{2}}$ 

= $\frac{30x+21y+22xy}{36x^{2}y^{2}}$

b) $\frac{x^{3}+2x}{x^{3}+1}$ + $\frac{2x}{x^{2}-x+1}$ + $\frac{1}{x+1}$

=$\frac{x^{3}+2x}{x^{3}+1}$ + $\frac{2x(x+1)}{x^{3}+1}$ + $\frac{x^{2}-x+1}{x^{3}+1}$ 

= $\frac{x^{3}+2x+2x^{2}+2x+x^{2}-x+1}{x^{3}+1}$ 

= $\frac{x^{3}+3x^{2}+3x+1}{x^{3}+1}$

= $\frac{(x+1)^{3}}{x^{3}+1} = \frac{(x+1)^{2}}{x^{2}-x+1}$

Bài tập 6.19 toán 8 tập 2 KNTT trang 9: 

a) Rút gọn biểu thức P = $\frac{x^{4}}{1-x}$ + $x^{3}$ + $x^{2}$ + $x$ + $1$ 

b) Tính giá trị của P tại x = -99

Đáp án:

a) P = $\frac{x^{4}}{1-x} + x^{3} + x^{2} + x + 1$

= $\frac{x^{4}+x^{3}(1-x)+x^{2}(1-x)+x(1-x)+(1-x)}{1-x}$

= $\frac{1}{1-x}$

b) Tại x = -99: P = $\frac{1}{100}$

Bài tập 6.20 toán 8 tập 2 KNTT trang 10: 

a) Rút gọn biểu thức Q = $\frac{18}{(x-3)(x^{2}-9)}$ - $\frac{3}{x^{2}-6x+9}$ - $\frac{x}{x^{2}-9}$.

b) Tính giá trị của Q tại x = 103

Đáp án:

a) Q = $\frac{18}{(x-3)(x^{2}-9)}$ - $\frac{3}{x^{2}-6x+9}$ - $\frac{x}{x^{2}-9}$

= $\frac{18}{(x-3)(x-3)(x+3)}$ - $\frac{3}{(x-3)^{2}}$ - $\frac{x}{(x-3)(x+3)}$

= $\frac{18}{(x-3)^{2}(x+3)}$ - $\frac{3(x+3)}{(x-3)^{2}(x+3)}$ - $\frac{x(x-3)}{(x-3)^{2}(x+3)}$

= $\frac{18-3x-9-x^{2}+3x}{(x-3)^{2}(x+3)}$

= $\frac{-x^{2}+9}{(x-3)^{2}(x+3)}$

= $\frac{-(x-3)(x+3)}{(x-3)^{2}(x+3)}$

= $\frac{-1}{x-3}$

b) Tại x = 103: Q = $\frac{-1}{100}$

Bài tập 6.21 toán 8 tập 2 KNTT trang 10: 

a) Chứng minh rằng nếu a, b, c $\neq$ 0, a + b + c = 0 thì $\frac{1}{ab}$ + $\frac{1}{bc}$ + $\frac{1}{ca}$ = 0

b) Chứng minh rằng nếu x $\neq$ y, y $\neq$ z, z $\neq$ x thì $\frac{1}{(x-y)(y-z)}$ + $\frac{1}{(y-z)(z-x)}$ + $\frac{1}{(z-x)(x-y)}$ = 0

Đáp án:

a) Ta có: $\frac{1}{ab}$ + $\frac{1}{bc}$ + $\frac{1}{ca}$

= $\frac{c}{abc}$ + $\frac{a}{abc}$ + $\frac{b}{abc}$

= $\frac{c + a + b}{abc}$

= $\frac{0}{abc}$

= 0 

b) Ta có: $\frac{1}{(x-y)(y-z)}$ + $\frac{1}{(y-z)(z-x)}$ + $\frac{1}{(z-x)(x-y)}$

= $\frac{z-x}{(x-y)(y-z)(z-x)}$ + $\frac{x-y}{(y-z)(z-x)(x-y)}$ + $\frac{y-z}{(z-x)(x-y)(y-z)}$

= $\frac{z-x+x-y+y-z}{(x-y)(y-z)(z-x)}$

= 0

Bài tập 6.22 toán 8 tập 2 KNTT trang 10: Cho biểu thức P = $\frac{x}{y-2}$ + $\frac{2x-3y}{x-6}$. Chứng minh rằng khi x, y thay đổi luôn thỏa mãn điều kiện 3y – x = 6 thì P có giá trị không đổi.

Đáp án:

Ta có: 3y – x = 6 suy ra x = 3y – 6

Thay x = 3y – 6 vào biểu thức P ta được: 

P = $\frac{3y-6}{y-2}$ + $\frac{2(3y-6)-3y}{3y-6-6}$

= 3 + $\frac{3y-12}{3y-12}$

= 3 + 1

= 4

Vậy với mọi giá trị của x, y thỏa mãn 3y – x = 6, P có giá trị không đổi (P = 4).

Bài tập 6.23 toán 8 tập 2 KNTT trang 10: 

Cho biểu thức P = $\frac{2x-6}{x^{3}-3x^{2}-x+3}$ + $\frac{2x^{2}}{1-x^{2}}$ - $\frac{6}{x-3}$ (x $\neq$ 3, x $\neq$ 1, x $\neq$ -1)

a) Rút gọn phân thức $\frac{2x-6}{x^{3}-3x^{2}-x+3}$

b) Chứng tỏ rằng có thể viết P = a + $\frac{b}{x-3}$ trong đó a, b là những hằng số.

c) Tìm tập hợp các giá trị nguyên của x để P có giá trị là số nguyên.

Đáp án: 

a) Ta có: $\frac{2x-6}{x^{3}-3x^{2}-x+3}$ 

= $\frac{2(x-3)}{x^{2}(x-3)-(x-3)}$

= $\frac{2(x-3)}{(x^{2}-1)(x-3)}$

= $\frac{2}{x^{2}-1}$

b) P = $\frac{2x-6}{x^{3}-3x^{2}-x+3}$ + $\frac{2x^{2}}{1-x^{2}}$ - $\frac{6}{x-3}$

= $\frac{2}{x^{2}-1}$ + $\frac{2x^{2}}{1-x^{2}}$ - $\frac{6}{x-3}$

= $\frac{2}{x^{2}-1}$ - $\frac{2x^{2}}{x^{2}-1}$ - $\frac{6}{x-3}$

= $\frac{-2(x^{2}-1)}{x^{2}-1}$ - $\frac{6}{x-3}$

= -2 + $\frac{-6}{x-3}$

Vậy P = a + $\frac{b}{x-3}$ = -2 + $\frac{-6}{x-3}$, với a = -2, b = -6

c) Ta có: P = -2 - $\frac{6}{x-3}$

Để P có giá trị là số nguyên thì $\frac{6}{x-3}$ phải có giá trị là số nguyên

Do đó (x-3) phải là ước số nguyên của 6

Loại x = 1 vì không thỏa mãn điều kiện đề bài

Vậy tập hợp các giá trị nguyên của x để P có giá trị là số nguyên là: {-3; 0; 2; 4; 5; 6; 9}

Bài tập 6.24 toán 8 tập 2 KNTT trang 10: 

a) Rút gọn biểu thức P = $\frac{x^{2}+2x}{x^{3}-1}$ - $\frac{1}{x^{2}-x}$ -$\frac{1}{x^{2}+x+1}$ (x $\neq$ 0, x $\neq$ 1)

b) Chứng tỏ rằng chỉ có một giá trị nguyên của x để P cũng nhận giá trị nguyên.

Đáp án:

a) P = $\frac{x^{2}+2x}{x^{3}-1}$ - $\frac{1}{x^{2}-x}$ -$\frac{1}{x^{2}+x+1}$

= $\frac{x^{2}+2x}{(x-1)(x^{2}+x+1)}$ - $\frac{1}{x(x-1)}$ - $\frac{1}{x^{2}+x+1}$

= $\frac{x(x^{2}+2x) - (x^{2}+x+1) - x(x-1)}{x(x-1)(x^{2}+x+1)}$

= $\frac{x^{3}+2x^{2} - x^{2}-x-1-x^{2}+x}{x(x-1)(x^{2}+x+1)}$

= $\frac{x^{3}-1}{x(x^{3}-1)}$

= $\frac{1}{x}$

b) Ta có: P = $\frac{1}{x}$

Để P nhận giá trị nguyên thì x phải là ước nguyên của 1, mặt khác x khác 1 (đề bài)
Suy ra x nhận giá trị là -1.

Vậy chỉ có một giá trị nguyên x = -1 để P cũng nhận giá trị nguyên (P = $\frac{1}{-1}$ = -1).

Bài tập 6.25 toán 8 tập 2 KNTT trang 10: 

Một tàu chở hàng đi từ cảng A đến cảng B cách nhau 900km với vận tốc không đổi là x (km/h). Khi đi được $\frac{1}{3}$ quãng đường thì một động cơ của tàu bị hỏng nên tàu chỉ còn chạy với vận tốc 12 km/h trong suốt 3 giờ tàu sửa chữa động cơ. Để về càng B không muộn hơn dự định. tàu phải tăng vận tốc thêm 5 km/h. Viết phân thức tính thời gian thực tế để tàu đi từ cảng A đến cảng B.

Đáp án:

Gọi thời gian thực tế để tàu đi từ cảng A đến cảng B là t (giờ), vận tốc ban đầu của tàu là x (km/h).

Tàu hỏng động cơ ở vị trí cách A là: $900 \cdot \frac{1}{3}$ = 300 (km)

Thời gian tàu đi 1/3 quãng đường đầu tiên (300 km) với vận tốc ban đầu x là: $\frac{300}{x}$ giờ

Theo đề bài: Khi đi được 1/3 quãng đường (300 km), tàu bị hỏng động cơ và chạy với vận tốc 12 km/h trong 3 giờ. Ta có tổng thời gian tàu dừng để sửa chữa động cơ là 3 giờ.

Quãng đường tàu chạy trong 3 giờ với tôc độ 12 km/h là 3.12 = 36 (km)

Quãng đường còn lại dài là: 900 – 300 – 36 = 564 (km) 

Sau khi sửa xong, để không muộn hơn dự định, tàu phải tăng vận tốc thêm 5 km/h. Ta có vận tốc mới của tàu là (x + 5) km/h.

Thời gian tàu chạy từ khi động cơ được sửa đến khi về cảng B là: $\frac{564}{x+5}$ giờ

Tổng thời gian thực tế từ cảng A đến cảng B là: t = $\frac{300}{x}$ + 3 + $\frac{564}{x+5}$ = $\frac{3x^{2}+879x+1500}{x(x+5)}$ (giờ)

Bài tập 6.26 toán 8 tập 2 KNTT trang 10: Cho hai hình hộp chữ nhật bằng nhau cùng có thể tích 200 $cm^{3}$ và một hình hộp chữ nhật có thể tích 500 $cm^{3}$ sắp xếp như trong hình bên (độ dài các cạnh hình hộp được tính bằng đơn vị cm). Viết các phân thức biểu thị độ dài (tính bằng cm) của các đoạn thẳng AC và DE.

Đáp án:

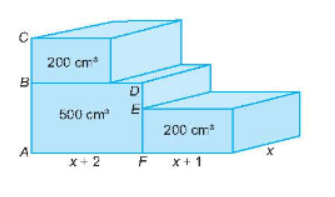
Hình hộp chữ nhật có thể tích 500 $cm^{3}$ có diện tích đáy là x(x+2) $cm^{2}$, suy ra độ dài chiều cao là: 

AB = DF = $\frac{500}{x(x+2)}$

Hình hộp chữ nhật có thể tích 200 $cm^{3}$ có diện tích đáy là x(x+1) $cm^{2}$, suy ra độ dài chiều cao là: 

EF = BC = $\frac{200}{x(x+1)}$

Vậy: AC = AB + BC = $\frac{500}{x(x+2)}$ + $\frac{200}{x(x+1)}$ (cm)

DE = DF – EF = $\frac{500}{x(x+2)}$ - $\frac{200}{x(x+1)}$ (cm)