Bài tập 9.1 toán 8 tập 2 KNTT trang 51: Khi viết $\triangle $ABC $\sim$ $\triangle $MNP thì góc nào của tam giác ABC tương ứng với góc PNM của tam giác MNP. Hãy viết các cặp góc bằng nhau và các cặp cạnh tương ứng tỉ lệ của hai tam giác đã cho.

Đáp án:

Khi viết $\triangle $ABC $\sim$ $\triangle $MNP thì góc CBA của tam giác ABC tương ứng với góc PNM của tam giác MNP.

Các cặp góc tương ứng bằng nhau: 

$\widehat{BAC} = \widehat{NMP}$

$\widehat{ABC} = \widehat{MNP}$

$\widehat{ACB} = \widehat{MPN}$

Các cặp cạnh tương ứng tỉ lệ:

$\frac{AB}{MN} = \frac{AC}{MP} = \frac{BC}{NP}$

Bài tập 9.2 toán 8 tập 2 KNTT trang 51: Cho $\triangle $ABC $\sim$ $\triangle $DEF. Những cách viết nào dưới đây đúng?

(1) $\triangle $BCA $\sim$ $\triangle $FED. 

(2) $\triangle $CBA $\sim$ $\triangle $EFD. 

(3) $\triangle $BAC $\sim$ $\triangle $EFD. 

(4) $\triangle $CBA $\sim$ $\triangle $FED. 

Đáp án:

Do các cặp đỉnh tương ứng là: A và D, B và E, C và F nên các cách viết (3) và (4) đúng, các cách viết (1) và (2) sai. 

Bài tập 9.3 toán 8 tập 2 KNTT trang 52: Với hai tam giác ABC và MNP bất kì sao cho $\triangle $ABC $\sim$ $\triangle $MNP. Những câu nào dưới đây đúng?

(1) AB = MN, AC = MP, BC = NP

(2) $\widehat{A} = \widehat{M}$

$\widehat{B} = \widehat{N}$

$\widehat{C} = \widehat{P}$

(3) $\frac{AB}{MN} = \frac{AC}{MP} = \frac{BC}{NP}$

(4) $\widehat{B} = \widehat{P}$

$\widehat{C} = \widehat{M}$

$\widehat{A} = \widehat{N}$

Đáp án:

Các câu (2) và (3) đúng, các câu (1) và (4) sai.

Bài tập 9.4 toán 8 tập 2 KNTT trang 52: Cho $\triangle $ABC $\sim$ $\triangle $A'B'C', biết $\widehat{A} = 60^{o}$, $\widehat{B’} = 50^{o}$. Hãy tính số đo các góc còn lại của tam giác ABC và tam giác A'B'C'.

Đáp án:

Ta có: $\widehat{A’} = \widehat{A} = 60^{o}$

$\widehat{B} = \widehat{B’} = 50^{o}$

$\widehat{C} = \widehat{C’} = 180^{o} - \widehat{A’} - \widehat{B’} = 180^{o} - 60^{o} - 50^{o} = 70^{o}$

Bài tập 9.5 toán 8 tập 2 KNTT trang 52: Cho $\triangle $ABC $\sim$ $\triangle $MNP. Biết AB = 5 cm, MN = 8 cm và chu vi tam giác ABC bằng 20 cm. Hỏi $\triangle $ABC $\sim$ $\triangle $MNP với tỉ số đồng dạng bằng bao nhiêu và chu vi tam giác MNP bằng bao nhiêu ?

Đáp án:

Ta có: $\frac{5}{8} = \frac{AB}{MN} = \frac{AC}{MP} = \frac{BC}{NP} = \frac{AB + AC + BC}{MN + MP + NP}$

Do $\triangle $ABC $\sim$ $\triangle $MNP với tỉ số đồng dạng bằng $\frac{5}{8}$ và chu vi của $\Delta ABC$ là 20 cm, suy ra chu vi tam giác MNP là: 

$ MN + MP + NP = \frac{8}{5}(AB + AC + BC) = \frac{8 \cdot 20}{5} = 32$ (cm)

Bài tập 9.6 toán 8 tập 2 KNTT trang 52: Cho tam giác ABC đồng dạng với một tam giác có ba đỉnh là D, E, F. Biết rằng $\widehat{A} > \widehat{B} = 60^{o} = \widehat{D} > \widehat{E}$, hãy chỉ ra các đỉnh tương ứng và viết đúng kí hiệu đồng dạng của hai tam giác đó.

Đáp án:

Do tổng các góc trong một tam giác bằng $180^{o}$ nên ta có:

$\widehat{A} > \widehat{B} = 60^{o} > \widehat{C}$

$\widehat{F} > \widehat{D} = 60^{o} > \widehat{E}$

Vì hai tam giác đồng dạng thì có các đỉnh tương ứng bằng nhau nên chỉ có thể xảy ra: 

$\widehat{A} = \widehat{F}$

$\widehat{B} = \widehat{D}$

$\widehat{C} = \widehat{E}$

Do đó $\triangle $ABC $\sim$ $\triangle $FDE.

Bài tập 9.7 toán 8 tập 2 KNTT trang 52: Cho tam giác không cân ABC đồng dạng với một tam giác có ba đỉnh là M, N, P. Biết rằng $\frac{AB}{NP} = \frac{AC}{PM} = \frac{BC}{MN}$, hãy chỉ ra các đỉnh tương ứng và viết đúng kí hiệu đồng dạng của hai tam giác đó.

Đáp án:

Ta thấy các cạnh cạnh tương ứng của hai tam giác đồng dạng đã cho là: AB và NP, AC và PM, BC và MN. Do các đỉnh tương ứng sẽ đối diện các cạnh tương ứng nên các cặp đỉnh tương ứng của hai tam giác đồng dạng đã cho là: C và M, B và N, A và P. 

Do đó $\triangle $ABC $\sim$ $\triangle $PNM.

Bài tập 9.8 toán 8 tập 2 KNTT trang 52: Trong Hình 9.3, cho PQ và MN cùng song song với AB. Hãy liệt kê ba cặp tam giác phân biệt đồng dạng với nhau.

Đáp án:

Do MN // AB nên $\triangle $CMN $\sim$ $\triangle $CAB.

Do PQ // AB nên $\triangle $CPQ $\sim$ $\triangle $CAB.

Do PQ // MN (cùng song song với AB) nên $\triangle $CPQ $\sim$ $\triangle $CMN.

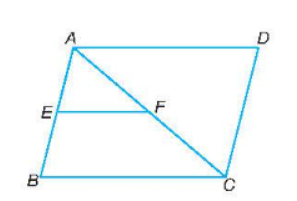
Bài tập 9.9 toán 8 tập 2 KNTT trang 52: Cho hình bình hành ABCD và cho E, F lần lượt là trung điểm của AB và AC. Chứng minh rằng $\triangle $AEF $\sim$ $\triangle $CDA.

Đáp án:

Ta có EF // BC (EF là đường trung bình của tam giác ABC) nên $\triangle $AEF $\sim$ $\triangle $ABC. với tỉ số đồng dạng bằng $\frac{AE}{AB} = \frac{1}{2}$

Mặt khác $\Delta ABC = \Delta CDA$ (c.c.c) nên $\triangle $ABC $\sim$ $\triangle $CDA với tỉ số đồng dạng bằng 1. 

Do đó $\triangle $AEF $\sim$ $\triangle $CDA với tỉ số đồng dạng bằng $\frac{1}{2}$

Bài tập 9.10 toán 8 tập 2 KNTT trang 52: Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng $\widehat{ABC} = \widehat{MNP}$ và BC =2NP. Chứng minh rằng  $ABC $\sim$ $\triangle $MNP và tìm tỉ số đồng dạng.

Đáp án:

Lấy E, F lần lượt là trung điểm của AB, AC. 

Khi đó  $ABC $\sim$ $\triangle $AEF với tỉ số đồng dạng bằng 2. 

Xét hai tam giác AEF và MNP, ta có:

$\widehat{AEF} = \widehat{ABC} = \widehat{MNP}$

$EF = \frac{BC}{2} = NP$

$\widehat{AFE} = \widehat{ACB} = \widehat{ABC} = \widehat{MNP} = \widehat{MPN}$

Vậy $\Delta AEF = \Delta MNP$ (g.c.g). Do đó  $AEF $\sim$ $\triangle $MNP với tỉ số đồng dạng bằng 1.

Vậy  $ABC $\sim$ $\triangle $MNP với tỉ số đồng dạng bằng 2.

Bài tập 9.11 toán 8 tập 2 KNTT trang 52: 

Cho tam giác ABC với AB = 6 cm, AC = 9 cm. 

a) Lấy các điểm M, N lần lượt trên các cạnh AB, AC sao cho AM = 4 cm, AN = 6 cm. Chứng minh rằng  $AMN $\sim$ $\triangle $ABC và tìm tỉ số đồng dạng.

b) Lấy điểm P trên cạnh AC sao cho AP = 4 cm. Chứng minh rằng $APB $\sim$ $\triangle $ABC.

Đáp án:

a) Ta có: $\frac{AM}{AB} = \frac{AN}{AC} = \frac{2}{3}$ 

Do đó theo định lí Thalès đảo áp dụng cho tam giác ABC và cát tuyến MN ta có: MN // AB. Vì vậy $AMN $\sim$ $\triangle $ABC.

b) Xét 2 tam giác APB và AMN, ta có: AP = AM, $\widehat{A}$ chung, AB = AN

Suy ra $APB $\sim$ $\triangle $AMN (c.g.c)

Do đó $APB $\sim$ $\triangle $ABC (tính chất bắc cầu)