BÀI 33. HAI TAM GIÁC ĐỒNG DẠNG (2 tiết)

I. ĐỊNH NGHĨA

HĐ1

Qua sát hình ảnh ta thấy:

AB=2DE;AC=2DF;BC=2EF 

=> $\frac{AB}{DE}$=$\frac{BC}{È}$=$\frac{AC}{DF}$=2

Khái niệm

Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:

$\frac{A'B'}{AB}$=$\frac{B'C'}{BC}$=$\frac{A'C'}{AC}$;

$\widehat{A'}$=$\widehat{A}$;$\widehat{B'}$=$\widehat{B}$;$\widehat{C'}$=$\widehat{C}$ 

Tam giác A'B'C' đồng dạng với tam giác ABC được kí hiệu ∆A'B'C' ∆ABC (viết theo thứ tự cặp đỉnh tương ứng).

Tỉ số k=$\frac{A'B'}{AB}$=$\frac{B'C'}{BC}$=$\frac{A'C'}{AC}$ được gọi là tỉ số đồng dạng của ∆A'B'C' với ∆ABC.

Nhận xét

+ Nếu ∆A'B'C' $\sim $∆ABC với tỉ số đồng dạng k thì ∆ABC $\sim $ ∆A'B'C' với tỉ số đồng dạng $\frac{1}{K}$. Do vậy khi ∆A'B'C' $\sim $ ∆ABC thì ta nói hai tam giác A'B'C' và ABC đồng dạng với nhau.

+ Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k=1. Đặc biệt, mọi tam giác đồng dạng với chính nó.

+ Nếu ∆A''B''C'' $\sim $ ∆A'B'C' với tỉ số đồng dạng k và ∆A'B'C' $\sim $ ∆ABC với tỉ số đồng dạng m thì ∆A''B''C'' $\sim $ ∆ABC với tỉ số đồng dạng k.m

Ví dụ 1: (SGK – tr.80)

Hướng dẫn giải (SGK – tr.80)

Luyện tập 1

Ta thấy ∆ABC $\sim $  ∆DEF với tỉ số đồng dạng k=2.

Hoặc: ∆DEF $\sim $  ∆ABC với tỉ số đồng dạng k=$\frac{1}{2}$.

Thử thách nhỏ

a) Vì ∆ABC $\sim $ ∆MNP => $\widehat{N}$=$\widehat{B}$ và $\widehat{C}$=$\widehat{P}$

Nếu ∆ABC cân tại A => $\widehat{B}$=$\widehat{C}$ => $\widehat{N}$=$\widehat{P}$

=> ∆MNP cân tại M.

b) $\widehat{M}$=$\widehat{A}$=60$^{\circ}$;$\widehat{N}$=$\widehat{B}$=60$^{\circ}$;$\widehat{P}$=$\widehat{C}$=60$^{\circ}$

=> ∆MNP đều.

c) Giả sử ∆ABC $\sim $ ∆MNP với hệ số đồng dạng k>0. Suy ra:

MN=$\frac{AB}{k}$≥MP=$\frac{AC}{k}$≥NP=$\frac{BC}{k}$ 

II. ĐỊNH LÝ

HĐ2

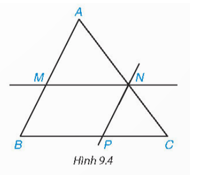
* Vì MN//BC (giả thiết)

Xét ∆ABC và ∆AMN có:

$\widehat{A}$ chung, tức là:$\widehat{BAC}$=$\widehat{MAN}$ (1)

$\widehat{AMN}$=$\widehat{ABC}$ ; $\widehat{ACB}$=$\widehat{ANM}$ (đồng vị) (2)

* Ta có MN//BP; NP//BM (giả thiết)

=> BMNP là hình bình hành => MN=BP.

=> $\frac{MN}{BC}$=$\frac{AN}{AC}$=$\frac{AN}{AB}$=$\frac{BP}{BC}$ (3)

* Từ (1)(2)(3) suy ra ∆ABC $\sim $ ∆AMN

Định lí:

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Chú ý:

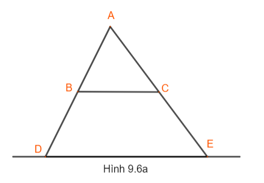
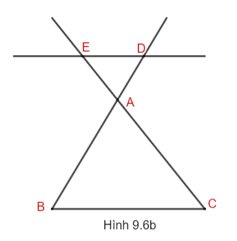
Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác. Chẳng hạn, trong Hình 9.6 có ED//BC. Khi đó, ∆ADE  $\sim $ ∆ABC.

Ví dụ 2: (SGK – tr.81)

Hướng dẫn giải (SGK – tr.81)

Luyện tập 2

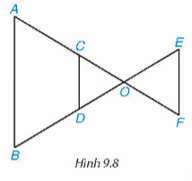
- Vì C∈OA;D∈OB và CD//AB nên ∆OCD $\sim $ ∆OAB

- Vì E∈OB;F∈OA và EF//AB nên ∆OEF $\sim $ ∆OBA

- Vì F∈OC;E∈OD và EF//CD nên ∆OEF $\sim $ ∆ODC

Vận dụng

- Vì CD//AB (cùng vuông góc với BC)

- Theo định lí trên thì ∆DEC $\sim $ ∆AEB

=> $\frac{DC}{AB}$=$\frac{EC}{EB}$ hay AB=$\frac{DC.EC}{EB}$

- Như vậy, chỉ cần đo chiều dài bóng cọc gỗ (đọa EC), khoảng cách EB thì với chiều cao CD đã biết, bác Dương tính được chiều cao AB.

Theo công thức trên, AB=5 m.