A. CÂU HỎI TRẮC NGHIỆM

Câu 1 toán 8 tập 2 KNTT trang 68: Câu nào sau đây là sai?

A. Hai tam giác có các cặp cạnh tương ứng tỉ lệ thì có các cặp góc tương ứng bằng nhau.  

B. Hai tam giác có các cặp góc tương ứng bằng nhau thì có các cặp cạnh tương ứng tỉ lệ.

C. Hai tam giác có một cặp góc tương ứng bằng nhau và hai cặp cạnh tương ứng tỉ lệ thì đồng dạng với nhau.

D. Hai tam giác cùng đồng dạng với một tam giác theo cùng một tỉ số đồng dạng thì bằng nhau.

Đáp án: C

Câu 2 toán 8 tập 2 KNTT trang 68: Bộ ba số đo nào dưới đây không là  độ dài ba cạnh của một tam giác vuông?

A. $\sqrt{2}$ cm, $\sqrt{2}$ cm, 2 cm.

B. 1 cm, 1 cm, $\frac{1}{\sqrt{2}}$ cm

C. 2 cm, 4 cm, $\sqrt{20}$ cm

D. 3 cm, 4 cm, 5 cm.

Đáp án: B

B. BÀI TẬP

Bài tập 9.61 toán 8 tập 2 KNTT trang 68: Cho $\triangle$ ABC $\sim$ $\triangle$ MNP với $\widehat{A} = 60^{o}$, $\widehat{N} = 40^{o}$. Hãy tính số đo các góc còn lại của hai tam giác ABC và MNP.

Đáp án:

Vì $\triangle$ ABC $\sim$ $\triangle$ MNP nên:

$\widehat{M} = \widehat{A} = 60^{o}$

$\widehat{B} = \widehat{N} = 40^{o}$

$\widehat{C} = \widehat{P} = 180^{o} - 60^{o} - 40^{o} = 80^{o}$

Bài tập 9.62 toán 8 tập 2 KNTT trang 68: Cho $\triangle$ ABC $\sim$ $\triangle$ MNP với AB = 5 cm, AC = 6 cm, BC= 7 cm. Biết rằng tam giác MNP có chu vi bằng 36 cm, hãy tính độ dài các cạnh của tam giác MNP và tỉ số đồng dạng của tam giác ABC với tam giác MNP.

Đáp án:

Vì $\triangle$ ABC $\sim$ $\triangle$ MNP nên:

$\frac{AB}{MN} = \frac{AC}{MP} = \frac{BC}{NP}$

= $\frac{AB +AC + BC}{MN + MP + NP} = \frac{5+6+7}{36} = \frac{1}{2}$

Do vậy $\triangle$ ABC $\sim$ $\triangle$ MNP với tỉ số đồng dạng $\frac{1}{2}$

MN = 2AB = 10 cm, MP = 2AC = 12 cm, NP = 2BC = 14 cm

Bài tập 9.63 toán 8 tập 2 KNTT trang 68: Cho tam giác ABC có AB = $\sqrt{15}$ cm, AC = 2BC. Tìm độ dài hai cạnh AC, BC sao cho ABC là một tam giác vuông.

Đáp án:

Nếu ABC là tam giác vuông thì thì BC không thể là cạnh huyền vì AC = 2BC > BC.

Suy ra tam giác ABC chỉ có thể vuông tại đỉnh B hoặc đỉnh C.

• Xét tam giác ABC vuông tại B:

Áp dụng đính lí Pythagore cho tam giác ABC vuông tại B, ta có

$AB^{2} + BC^{2} = AC^{2} = 4BC^{2}$

Suy ra $BC = \frac{AB}{\sqrt{3}}$ = $\sqrt{5}$ cm

$AC = 2BC = 2\cdot\sqrt{5}$ cm

Ngược lại, nếu BC = $\sqrt{5}$ cm; $AC = 2\cdot\sqrt{5}$ cm thì

$AB^{2} + BC^{2} = AC^{2}$

Do đó tam giác ABC vuông tại B (định lí Pythagore đảo)

• Xét tam giác ABC vuông tại C:

Áp dụng đính lí Pythagore cho tam giác ABC vuông tại C, ta có

$BC^{2} + AC^{2} = AB^{2} = 5BC^{2}$

Suy ra $BC = \frac{AB}{\sqrt{5}} = \sqrt{3}$ cm

$AC = 2BC = 2\cdot\sqrt{3}$ cm

Ngược lại, nếu $BC = \sqrt{3}$ cm; $AC =  2\cdot\sqrt{3}$ cm thì

$BC^{2} + AC^{2} = AB^{2}$

Do đó tam giác ABC vuông tại C (định lí Pythagore đảo)

Vậy để tam giác ABC vuông thì $BC = \sqrt{5}$ cm; $AC =  2\cdot\sqrt{5}$ cm hoặc $BC = \sqrt{3}$ cm; $AC =  2\cdot\sqrt{3}$ cm.

Bài tập 9.64 toán 8 tập 2 KNTT trang 68: Cho tam giác ABC với AB > AC. Lấy điểm D trên cạnh BC sao cho AC = AD. Qua D kẻ đường thẳng song song với BC và cắt AC tại E. Qua E kẻ đường thẳng song song với CD và cắt AB tại F. Chứng minh rằng:

a) $AD^{2} = AF\cdot AB$

b) $\triangle$ ACF $\sim$ $\triangle$ ABC

Đáp án:

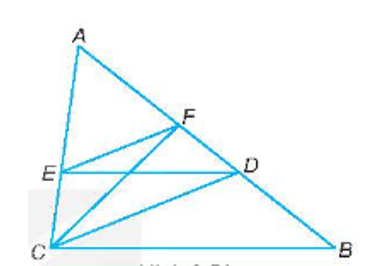
a) Do DE // BC nên $\triangle$ ADE $\sim$ $\triangle$ ABC

Suy ra $\frac{AD}{AB} = \frac{AE}{AC}$

hay $AD = \frac{AB \cdot AE}{AC}$ (1)

Do EF // CD nên $\triangle$ AEF $\sim$ $\triangle$ ACD

Suy ra $\frac{AF}{AD} = \frac{AE}{AC}$

hay $AD = \frac{AF \cdot AC}{AE}$ (2)

Nhân 2 vế tương ứng của đẳng thức (1) và (2) ta được:

$AD^{2} = AF \cdot AB$

b) Hai tam giác ACF và ABC có

$\frac{AC}{AB} = \frac{AE}{AD} = \frac{AE}{AC} = \frac{AF}{AC}$ (AC = AD nên AE = AF)

$\widehat{A}$ chung

Suy ra $\triangle$ ACF $\sim$ $\triangle$ ABC (c.g.c)

Bài tập 9.65 toán 8 tập 2 KNTT trang 69: Cho tam giác ABC vuông tại A (AC > AB), có AD là đường phân giác của góc A (D thuộc BC). Qua D kẻ đường thẳng vuông góc với BC và cắt cạnh AC tại E và cắt tia BA tại F. Chứng minh rằng:

a) $\triangle$ BDF $\sim$ $\triangle$ EDC

b) DB = DE

Đáp án:

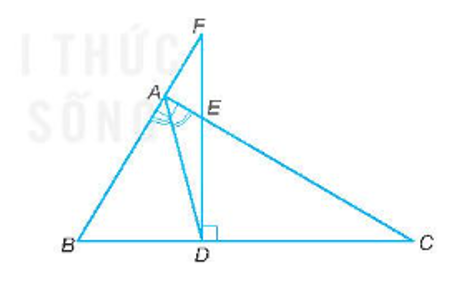
a) Hai tam giác vuông BDF (vuông tại D) và EDC (vuông tại D) có

$\widehat{FBD} = 90^{o} - \widehat{DCE} = \widehat{CED}$

Suy ra $\triangle$ BDF $\sim$ $\triangle$ EDC (một cặp góc nhọn bằng nhau)

b) Hai tam giác vuông ABC (vuông tại A) và DEC (vuông tại D) có

$\widehat{C}$ chung

Suy ra $\triangle$ ABC $\sim$ $\triangle$ DEC (một cặp góc nhọn bằng nhau)

Suy ra $\frac{AB}{DE} = \frac{AC}{DC}$

Mặt khác vì AD là phân giác của góc BAC nên

$\frac{AC}{DC} = \frac{AB}{BD}$

Suy ra $\frac{AB}{DE} = \frac{AB}{BD}$

Suy ra BD = DE.

Bài tập 9.66 toán 8 tập 2 KNTT trang 69: Cho tam giác ABC vuông tại A có đường cao AH.

a) Biết AB = 3 cm, AC = 4 cm, hãy tính độ dài các đoạn thẳng  AH, BH, CH.

b) Gọi M, N lần lượt là chân các đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng $\triangle$ HMN $\sim$ $\triangle$ ABC

Đáp án:

a) Áp dụng đính lí Pythagore cho tam giác ABC vuông tại A, ta có

$AB^{2} + AC^{2} = BC^{2} = 9 + 16 = 25$

Suy ra BC = 5 cm. Mặt khác $AH\cdot BC = AB \cdot AC$

Suy ra $AH = \frac{AB \cdot AC}{BC} = \frac{3 \cdot 4}{5} = 2,4 cm

Hai tam giác vuông ABC (vuông tại A) và HBA (vuông tại H) có

$\widehat{B}$ chung

Suy ra $\triangle$ ABC $\sim$ $\triangle$ HBA (một cặp góc nhọn bằng nhau)

Suy ra $\frac{AB}{BC} = \frac{HB}{BA}$

Hay $BH = \frac{AB^{2}}{BC} = \frac{3 \cdot 3}{5} = 1,8$ cm

Tương tự: $CH = \frac{AC^{2}}{BC} = \frac{4 \cdot 4}{5} = 3,2$ cm

b) Do AMHN là hình bình hành có một góc vuông nên là hình chữ nhật. Vì vậy ta có $\widehat{MHN} = 90^{o}$.

Mặt khác, do HM // AC nên theo định lí Thalès ta có:

$\frac{HM}{AC} = \frac{BH}{BC} = \frac{AB^{2}}{BC^{2}}$

Suy ra $\frac{HM}{AB} = \frac{AB \cdot AC}{BC^{2}}$

Tương tự $\frac{HN}{AC} = \frac{AB \cdot AC}{BC^{2}}$

Hai tam giác vuông HMN (vuông tại H) và ABC (vuông tại A) có

$\frac{HM}{AB} = \frac{HN}{AC}$

Suy ra $\triangle$ HMN $\sim$ $\triangle$ ABC (hai cặp cạnh góc vuông tỉ lệ)

Bài tập 9.67 toán 8 tập 2 KNTT trang 69: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:

a) $\triangle$ MNP $\sim$ $\triangle$ ABC và tìm tỉ số đồng dạng

b) $\triangle$ ABN $\sim$ $\triangle$ CAM và $\triangle$ ACP $\sim$ $\triangle$ BAM.

c) $AN \bot CM$ và $AP \bot BM$

Đáp án:

a) Do MN, MP lần lượt là các đường trung bình của tam giác HAB và tam giác HAC nên $\frac{MN}{AB} = \frac{MP}{AC} = \frac{1}{2}$

Mặt khác $\frac{NP}{BC} = \frac{HN + HP}{HB + HC} = \frac{1}{2}$

Như vậy hai tam giác MNP và ABC có:

$\frac{MN}{AB} = \frac{MP}{AC} = \frac{NP}{BC} = \frac{1}{2}$

Suy ra $\triangle$ MNP $\sim$ $\triangle$ ABC (c.c.c) vơi tỉ số đồng dạng bằng $\frac{1}{2}$

b) Hai tam giác vuông ABH (vuông tại H) và CAH (vuông tại H) có

$\widehat{ABH} = 90^{o} - \widehat{ACH} = \widehat{CAH}$

Suy ra $\triangle$ ABH $\sim$ $\triangle$ CAH (một cặp góc nhọn bằng nhau)

Suy ra $\frac{AB}{AC} = \frac{BH}{AH} = \frac{BN}{AM}$

Hai tam giác ABN và CAM có

$\widehat{ABN} = \widehat{ABH} = \widehat{CAH} = \widehat{CAM}$

$\frac{AB}{CA} = \frac{BN}{AM}$ (cmt)

Suy ra $\triangle$ ABN $\sim$ $\triangle$ CAM

Tương tự: $\triangle$ ACP $\sim$ $\triangle$ BAM

c) Xét tam giác ANC có $AM \bot CN$, $NM \bot AC$ (vì MN // AB mà $AB \bot AC$)

Suy ra ba đường cao của tam giác ANC đồng quy tại điểm M

Suy ra $CM \bot AN$

Tương tự: $BM \bot AP$

Bài tập 9.68 toán 8 tập 2 KNTT trang 69: Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB. Chứng minh rằng $\triangle$ CAM $\sim$ $\triangle$ CBN và $\triangle$ CHM $\sim$ $\triangle$ CAN.

Đáp án:

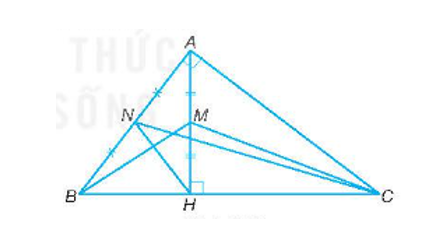
Hai tam giác vuông CAH (vuông tại H) và CBA (vuông tại A) có

$\widehat{C}$ chung

Suy ra $\triangle$ CAH $\sim$ $\triangle$ CBA (một cặp góc nhọn bằng nhau)

Suy ra $\frac{CA}{CB} = \frac{AH}{BA} = \frac{AM}{BN}$

$\widehat{CAH} = \widehat{CBA}$

Hai tam giác CAM và CBN có

$\frac{CA}{CB} = \frac{AM}{BN}$ (cmt)

$\widehat{CAM} = \widehat{CAH} = \widehat{CBA} = \widehat{CBN}$ (cmt)

Suy ra $\triangle$ CAM $\sim$ $\triangle$ CBN (c.g.c)

Hai tam giác vuông CHM (vuông tại H) và CAN (vuông tại A) có

$\frac{HC}{AC} = \frac{HA}{AB} = \frac{HM}{AN}$

Suy ra $\triangle$ CHM $\sim$ $\triangle$ CAN (2 cặp cạnh góc vuông tỉ lệ)

Bài tập 9.69 toán 8 tập 2 KNTT trang 69: Vẽ lại Hình 9.18 vào vở và vẽ tứ giác A’B’C’D’ là hình đồng dạng phối cảnh của tứ giác ABCD theo tỉ số dồng dạng $\frac{3}{2}$ và tâm phối cảnh là điểm O.

Đáp án:

Trên các tia OA, OB, OC, OD lần lượt lấy các điểm A’, B’, C’, D’ sao cho

$OA’ = \frac{3}{2}OA$

$OB’ = \frac{3}{2}OB$

$OC’ = \frac{3}{2}OC$

$OD’ = \frac{3}{2}OD$

Vẽ các đoạn thẳng A’B’, B’C’, C’D’, D’A’ ta được tứ giác A’B’C’D’ là hình đồng dạng phối cảnh của tứ giác ABCD với tâm phối cảnh O và tỉ số đồng dạng bằng $\frac{3}{2}$.