BÀI 36. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC VUÔNG 

I. ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG

Định lí 1

Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đóc đồng dạng với nhau.

Định lí 2

Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

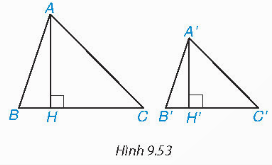
∆ABC vuông tại A, ∆A'B'C' vuông tại A

+ Nếu $\widehat{B'}$=$\widehat{AB}$ thì ∆A'B'C'  $\sim $ ∆ABC.

+ Nếu $\frac{A'B'}{AB}$=$\frac{A'C'}{AC}$ thì ∆A'B'C' $\sim $ ∆ABC.

Câu hỏi

- Hai tam giác vuông ABC (vuông tại A) và XYZ (vuông tại X) có $\widehat{B}$=$\widehat{Z}$=60$^{\circ}$ nên ∆ABC $\sim $ ∆XYZ.

- Hai tam giác vuông DEF (vuông tại D) và GKH (vuông tại G) có:

$\frac{DE}{GK}$=$\frac{DF}{GH}$=$\frac{1}{2}$ nên ∆DEF $\sim $ ∆GKH.

Ví dụ 1: (SGK – tr.91)

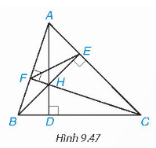
Hướng dẫn giải (SGK – tr.91)

Luyện tập 1

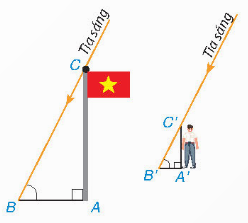
a) Xét ∆ABC (vuông tại A) và ∆A'B'C' (vuông tại A') có: $\widehat{B}$=$\widehat{B'}$

Nên ∆ABC $\sim $ ∆A'B'C'

b) Theo giả thiết, ta có:

AB=6 m, A'B'=0,7 m, A'C'=1,4 m.

Từ phần a) ta suy ra:

$\frac{AB}{A'B'}$=$\frac{AC}{A'C'}$ => AC=$\frac{AB.A'C'}{A'B'}$=12 (m)

Thử thách nhỏ

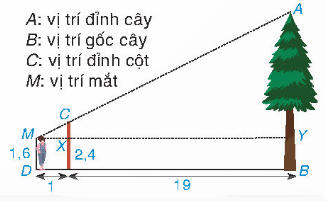
Ta có: CX=2,4-1,6=0,8 (m)

MN=1+19=20 (m)

Xét ∆MXC (vuông tại X) và ∆MYA (vuông tại Y) có: $\widehat{M}$ chung.

=> ∆MXC $\sim $ ∆MYA => $\frac{MX}{MY}$=$\frac{XC}{YA}$

=> YA=20.0,8=16 (m)

=> AB=BY+YA=1,6+16=17,6 m

II. TRƯỜNG HỢP ĐỒNG DẠNG ĐẶC BIỆT CỦA HAI TAM GIÁC

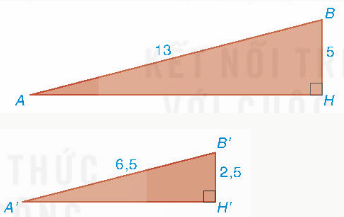
HĐ1

- $\frac{A'B'}{AB}$=$\frac{B'H'}{BH}$=$\frac{1}{2}$

- AH$^{2}$=AB$^{2}$-BH$^{2}$=144

=> AH=12 (m)

- A'H'$^{2}$=A'B'$^{2}$-B'H'$^{2}$=36

=> AH=6 (m)

- $\frac{A'H'}{AH}$=$\frac{1}{2}$=$\frac{B'H'}{BH}$ và do đó hai tam giác vuông A'H'B' và AHB đồng dạng

=> $\widehat{A}$=$\widehat{A'}$. Vậy hai con dốc có độ dốc như nhau.

Định lí

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

Chứng minh định lí (SGK – tr.101)

Hướng dẫn giải (SGK – tr.101)

Câu hỏi

+) ∆ACB $\sim $ ∆DEF vì $\frac{AC}{DE}$=$\frac{BC}{FE}$=$\frac{3}{2}$

Ví dụ 2: (SGK – tr.101)

Hướng dẫn giải (SGK – tr.101)

Nhận xét

Nếu ∆A'B'C' ∆ABC theo tỉ số k và AH, A'H' lần lượt là các đường cao của ∆ABC và ∆A'B'C' thì ∆A'B'H' ∆ABH (do $\widehat{B'}$=$\widehat{B}$) theo tỉ số k và $\frac{A'H'}{AH}$=k.

Luyện tập 2

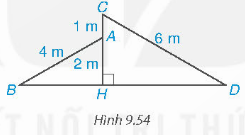
Xét ∆ABH (vuông tại H) và ∆CDH (vuông tại H) có:

$\frac{AB}{CD}$=$\frac{2}{3}$=$\frac{AH}{CH}$ => ∆ABH $\sim $ ∆CDH

=> $\widehat{ABD}$=$\widehat{ABH}$=$\widehat{CDH}$=$\widehat{CDB}$

Vậy $\widehat{ABD}$=$\widehat{CDB}$.

Vận dụng

- Gọi x (cm) là độ dài của chiều ngang màn hình chiếc tivi 55 inch.

- Có 55 inch =139,7 cm; 32 inch = 81,28 cm.

- Chiếc ti vi cũ có: 

+ Chiều ngang màn hình là 72 cm

+ Đường chéo của tivi là: 32 . 2,54=81,28 cm

- Có $\frac{81,28}{139,7}$=$\frac{72}{X}$ => x=123,75 cm =1,2375 m.

Vậy không thể đặt vừa chiếc ti vi vào khoảng trống hình vuông cạnh 1 m.