BÀI 34. BA TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC (3 tiết)

I. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT CỦA TAM GIÁC

Trường hợp đồng dạng cạnh – cạnh – cạnh

HĐ1

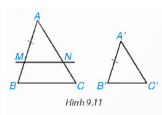
a) Nếu A'B'=AB thì A'C'=AC và B'C'=BC

=> ∆A'B'C'=∆ABC (c.c.c)

Do đó ∆A'B'C'  $\sim $ ∆ABC

b) ∆AMN $\sim $  ∆ABC vì MN//BC.

$\frac{AN}{AC}$=$\frac{AM}{AB}$=$\frac{A'B'}{AB}$=$\frac{A'C'}{AC}$=> AN=A'C'

$\frac{MN}{BC}$=$\frac{AM}{AB}$=$\frac{A'B'}{AB}$=$\frac{B'C'}{BC}$ => MN=B'C'

=> ∆AMN=∆A'B'C'

- Vì ∆AMN $\sim $ ∆ABC (do MN//BC) nên ∆A'B'C' ∆ABC

c) Nếu A'B'>AB, bằng cách đổi vai trò ∆ABC và ∆A'B'C' cho nhau thì theo phần b) ∆ABC $\sim $ ∆A'B'C'.

Định lí

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Câu hỏi

+ ∆ABC $\sim $ ∆HGK (c.c.c). Vì: $\frac{AB}{HG}$=$\frac{BC}{GK}$=$\frac{AC}{HK}$=$\frac{1}{2}$

+ ∆DEF $\sim $ ∆MNP (c.c.c). Vì:$\frac{DE}{MN}$=$\frac{EF}{NP}$=$\frac{DF}{MP}$=$\frac{1}{2}$

Ví dụ 1: (SGK – tr.84)

Hướng dẫn giải (SGK – tr.84)

Luyện tập 1

+ ∆ABC:

AC=18-AB-BC=18-4-6=8 cm

+ ∆DEF:

EF=27-DE-FD=27-6-12=9 cm

Xét ∆ABC và ∆DEF có:

$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$=23 => ∆ABC $\sim $ ∆DEF (c.c.c)

Vận dụng

- Vẽ ∆ABC với các số đo: AB=2;BC=3;AC=4 (cm)

Gọi Điểm đặt trái bóng là M, Chân hai cột gôn là N và P. Thì ta có hình minh họa:

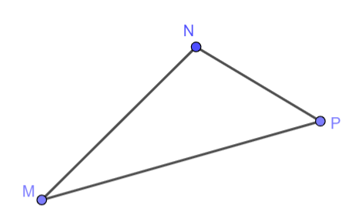
Ta có: NP :NM :MP=2 :3 :4=BC :BA :AC

=> ∆ABC$\sim $  ∆MNP (c.c.c)

=> $\widehat{A}$=$\widehat{M} \approx $29$^{\circ}$ 

II. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI CỦA TAM GIÁC

Trường hợp đồng dạng cạnh – góc – cạnh

HĐ2

+ $\frac{A'B'}{AB}$=$\frac{A'C'}{AC}$=32

+ BC ≈2,6 cm; B'C'≈3,9 cm

=> $\frac{B'C'}{BC}$=32

+ ∆A'B'C' $\sim $ ∆ABC với tỉ số đồng dạng là k=$\frac{3}{2}$

Định lí (trường hợp đồng dạng cạnh – góc – cạnh)

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

Chứng minh định lí (SGK – tr.86).

Câu hỏi

+) ∆ABC $\sim $ ∆MNP (c.g.c)

Vì: $\frac{AC}{MP}$=$\frac{AB}{MN}$=$\frac{1}{2}$ và $\widehat{A}$=$\widehat{M}$=70$^{\circ}$

Ví dụ 2: (SGK – tr.86)

Hướng dẫn giải (SGK – tr.86)

Nhận xét

Nếu ∆A'B'C' $\sim $ ∆ABC theo tỉ số k và AM, A'M' lần lượt là các đường trung truyến của ∆ABC và ∆A'B'C' thì $\frac{A'M'}{AM}$=k.

Luyện tập 2

Vì ∆A'B'C' $\sim $ ∆ABC nên $\widehat{A'B'C'}$=$\widehat{ABC}$ và  $\frac{A'B'}{AB}$=$\frac{B'C'}{BC}$. Do đó:

$\frac{M'B'}{MB}$=$\frac{M'C'}{MC}$=$\frac{M'B'-M'C'}{MB-MC}$=$\frac{B'C'}{BC}$=$\frac{A'B'}{AB}$

Xét ∆A'B'M' và ∆ABM có:

$\frac{A'B'}{AB}$=$\frac{B'M'}{BM}$

$\widehat{A'B'M'}$=$\widehat{A'B'C'}$=$\widehat{ABC}$=$\widehat{ABM}$ 

=> ∆A'B'M' $\sim $ ∆ABM (c.g.c)

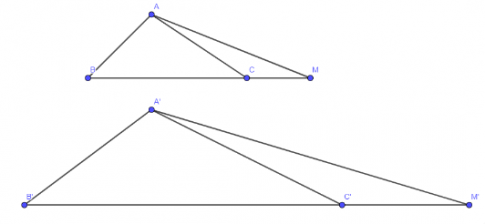
Tranh luận

Bạn Lan nhận xét không đúng.

Ví dụ:

Lấy ∆ABC  $\sim $ ∆A'B'C' với $\widehat{C'}$=$\widehat{M}$<90$^{\circ}$ 

Lấy C trên đoạn MB sao cho ∆AMC cân tại A (Hình 9.16)

=> ∆ABC và ∆A'B'C' không đồng dạng

III. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA CỦA TAM GIÁC

Trường hợp đồng dạng góc – góc

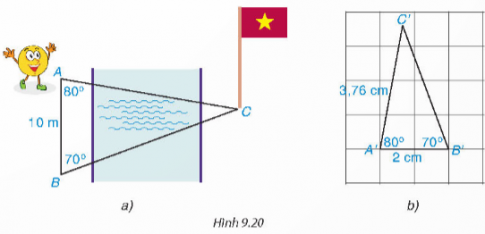
HĐ3

- Hai tam giác này có hình dạng rất giống nhau (chỉ khác về kích thước) nên chúng rất có khả năng đồng dạng với nhau.

Khi đó tỉ số đồng dạng bằng:$\frac{A'B'}{AB}$=$\frac{2}{1000}$=$\frac{1}{500}$

HĐ4

Nếu ∆A'B'C' $\sim $ ∆ABC và A'C'=3,76 cm 

$\frac{A'C'}{AC}$=$\frac{A'B'}{AB}$ ta suy ra:

AC=$\frac{A'C'}{A'B'}$' . AB=$\frac{3,76}{2}$ . 10=18,8 (m)

Định lí (trường hợp đồng dạng góc – góc)

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Chứng minh định lí (SGK – tr.88)

Câu hỏi

+) ∆ABC  $\sim $ ∆DEF (g.g) vì $\widehat{A}$=$\widehat{D}$=60$^{\circ}$ và $\widehat{B}$=$\widehat{E}$=50$^{\circ}$

Theo định lí Tổng ba góc trong một tam giác:

$\widehat{P}$=180$^{\circ}$-$\widehat{M}$-$\widehat{N}$=50$^{\circ}$ 

Do đó:

+) ∆ABC $\sim $ ∆MPN (g.g) vì $\widehat{A}$=$\widehat{M}$=60$^{\circ}$ và $\widehat{B}$=$\widehat{P}$=50$^{\circ}$

+) ∆DEF $\sim $  ∆MPN (g.g) vì $\widehat{D}$=$\widehat{M}$=60$^{\circ}$ và $\widehat{E}$=$\widehat{P}$=50$^{\circ}$.

Ví dụ 3: (SGK – tr.89)

Hướng dẫn giải (SGK – tr.89)

Nhận xét

Nếu ∆A'B'C' $\sim $ ∆ABC theo tỉ số k và AM, A'M' lần lượt là các đường phân giác của ∆ABC và ∆A'B'C' thì $\frac{A'M'}{AM}$=k.

Luyện tập 3

Xét ∆ABC và ∆ADB có:

$\widehat{ABC}$=$\widehat{ADB}$ (giả thiết)

$\widehat{A}$ chung

=> ∆ABC $\sim $ ∆ADB (g.g)

=> $\frac{AB}{AD}$=$\frac{AC}{AB}$ => AB$^{2}$=AD.AC (đpcm).

Thử thách nhỏ

1. Do tổng các góc trong một tam giác bằng 180o nên:

$\frac{\widehat{A'}+\widehat{\leftarrow B'}}{2}$=180$^{\circ}$-$\widehat{A'I'B'}$=180o-$\widehat{AIB}$=$\frac{\widehat{A}+\widehat{\leftarrow B}}{2}$ 

=> $\widehat{A'}$+$\widehat{B'}$=$\widehat{A}$+$\widehat{B}$. Do đó:

$\widehat{C'}$=180$^{\circ}$=$\widehat{A'}$-$\widehat{B'}$=180o-$\widehat{A}$-$\widehat{B}$=$\widehat{C}$ 

Tương tự, $\widehat{B'}$=$\widehat{B}$.

Vậy ∆A'B'C' $\sim $ ∆ABC (g.g) ($\widehat{B'}$=$\widehat{B}$;$\widehat{C'}$=$\widehat{C}$).

2. Nếu $\widehat{C}$, $\widehat{C'}$ đều nhọn: 

Lấy điểm M trên tia BC sao cho ∆ABM $\sim $ ∆A'B'C'.

* Giả sử điểm C không trùng với M. Khi đó ∆A'B'C' $\sim $ ∆ABM => $\frac{A'C'}{AM}$=$\frac{A'B'}{AB}$=$\frac{A'C'}{AC}$ 

=> AM=AC => ∆AMC cân tại A.

+ Nếu M nằm giữa B và C thì:

$\widehat{AMB}$=180$^{\circ}$-$\widehat{AMC}$=180$^{\circ}$-$\widehat{ACM}$>90$^{\circ}$>$\widehat{A'C'M'}$=> Vô Lý.

+ Vậy C nằm giữa B và M (Hình 9.19). Khi đó $\widehat{ACB}$=180$^{\circ}$-$\widehat{ACM}$=180$^{\circ}$-$\widehat{AMB}$=180$^{\circ}$-$\widehat{C'}$>90$^{\circ}$ => Vô Lý.

=> Vậy điểm C phải trùng với M và ∆ A'B'C' $\sim $ ∆ABC.