Giải bài tập 4.17 trang 55 SBT toán 8 tập 1 kết nối:

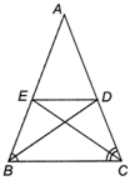
Trong ∆ABC có BD là phân giác của $\widehat{ABC}$ nên $\frac{DA}{DC}=\frac{BA}{BC}$ (tính chất đường phân giác của tam giác). (1)

Trong ∆ABC có CE là phân giác của $\widehat{ACB}$ nên $\frac{EA}{EB}=\frac{CA}{BB}$ (tính chất đường phân giác của tam giác). (2)

Mà ∆ABC cân tại A nên AB = AC  (3)

Từ (1), (2), (3), suy ra: $\frac{DA}{DC}=\frac{EA}{EB}$

Xét DABC có $\frac{DA}{DC}=\frac{EA}{EB}$ suy ra ED // BC (định lí Thales đảo).