Giải câu 10 trang 54 SBT toán 8 tập 1 kết nối:

Đáp án đúng là: B

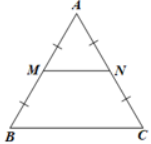
Trong ∆ABC có M, N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của ∆ABC

=> $MN=\frac{1}{2}BC$ (tính chất đường trung bình của tam giác)

=> $MN=\frac{1}{2}.3=1,5$ (cm)

Do ∆ABC đều nên AB = AC

Lại có M, N lần lượt là trung điểm của AB và AC nên $BM=\frac{1}{2}AB=\frac{1}{2}AC=CN$

Hay $BM=CN=\frac{1}{2}.3=1,5 (cm)$

Vậy chu vi của tứ giác BMNC là:

BM + MN + NC + BC = 1,5 + 1,5 + 1,5 + 3 = 7,5 (cm).