Dễ hiểu giải Toán 12 Kết nối bài 6: Vectơ trong không gian
Giải dễ hiểu bài 6: Vectơ trong không gian. Trình bày rất dễ hiểu, nên tiếp thu Toán 12 Kết nối dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 6: VECTƠ TRONG KHÔNG GIAN
1. VECTƠ TRONG KHÔNG GIAN
Hoạt động 1: Nhận biết vectơ trong không gian
Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ.
- Các đoạn thẳng này cho biết gì về hướng và độ lớn của các lực căng dây?
- Các đoạn thẳng này có cùng nằm trong một mặt phảng không?
Giải nhanh:
- Các đoạn thẳng này có hướng lên trên
Độ dài của các đoạn thẳng thể hiện cho độ lớn của các lực căng dây và được lấy tỉ lệ với độ lớn của các lực căng dây.
- Không cùng nằm trên một mặt phẳng.
Luyện tập 1: Cho hình lập phương ![]() (H.2.6). Trong các vectơ
(H.2.6). Trong các vectơ ![]() ,
, ![]() ,
, ![]() :
:
- Hai vectơ nào có giá cùng nằm trong mặt phẳng
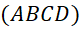 ?
? - Hai vectơ nào có cùng độ dài?

Giải nhanh:
 và
và 
- Vì
 là hình lập phương nên
là hình lập phương nên  .
.
Tam giác ![]() vuông tại
vuông tại ![]() nên
nên![]()
Tam giác ![]() vuông tại
vuông tại ![]() nên
nên![]()
=> ![]() hay
hay 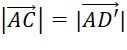 .
.
Vậy hai vectơ![]() và
và ![]() có cùng độ dài.
có cùng độ dài.
Hoạt động 2: Hình thành khái niệm hai vectơ cùng phương, cùng hướng/ngược hướng, hai vectơ bằng nhau trong không gian.
Cho hình hộp ![]() (H.2.7).
(H.2.7).
- So sánh độ dài của hai vectơ
 và
và  .
. - Nhận xét về giá của hai vectơ
 và
và  .
. - Hai vectơ
 và
và  có cùng phương không? Có cùng hướng không?
có cùng phương không? Có cùng hướng không?

Giải nhanh:
 .
.- Giá của
 và
và  song song với nhau.
song song với nhau.  và
và  cùng phương và cùng hướng.
cùng phương và cùng hướng.
Luyện tập 2: Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành.
là hình bình hành.
- Trong ba vectơ
 ,
,  và
và  , vectơ nào bằng vectơ
, vectơ nào bằng vectơ  ?
? - Gọi
 là một điểm thuộc cạnh
là một điểm thuộc cạnh 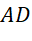 . Xác định điểm
. Xác định điểm  sao cho
sao cho  .
.
Giải nhanh:
a) ![]() là hình bình hành =>
là hình bình hành => ![]() , AB = CD =>
, AB = CD => ![]() =
= ![]()
![]() và
và ![]() chéo nhau =>
chéo nhau => ![]() và
và ![]() không cùng phương =>
không cùng phương =>![]()
![]() và
và ![]() không cùng phương =>
không cùng phương => ![]() và
và ![]() không bằng nhau.
không bằng nhau.
- Qua
 vẽ đường thẳng song song với
vẽ đường thẳng song song với  cắt
cắt 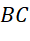 tại
tại  .
.
Tứ giác ![]() có:
có: ![]() ,
, ![]() =>
=> ![]() là hình bình hành =>
là hình bình hành => ![]() .
.
Mà ![]() =>
=> ![]() và
và ![]() cùng độ dài và cùng hướng =>
cùng độ dài và cùng hướng => ![]() .
.
Vậy điểm ![]() cần tìm là giao điểm của đường thẳng qua
cần tìm là giao điểm của đường thẳng qua ![]() song song với
song song với ![]() và cạnh
và cạnh ![]() .
.
Vận dụng 1: Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.
Giải nhanh:
Gọi vectơ biểu diễn độ dịch chuyển của thang máy từ tầng 15 lên tầng 22 của tòa nhà là ![]() , tầng 22 lên tầng 29 của tòa nhà là
, tầng 22 lên tầng 29 của tòa nhà là ![]() .
.
Vì ![]() và
và ![]() đều dịch chuyển từ tầng thấp lên tầng cao =>
đều dịch chuyển từ tầng thấp lên tầng cao => ![]() và
và ![]() có cùng hướng (1)
có cùng hướng (1)
Độ dài vectơ ![]() là:
là: ![]() , độ dài vectơ
, độ dài vectơ ![]() là:
là: ![]() =>
=> ![]() (2)
(2)
(1) và (2) => ![]() .
.
Vậy các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau.
2. TỔNG VÀ HIỆU CỦA HAI VECTƠ TRONG KHÔNG GIAN
Hoạt động 3: Hình thành khái niệm tổng của hai vectơ trong không gian.
Trong không gian, cho hai vectơ ![]() và
và ![]() không cùng phương. Lấy điểm
không cùng phương. Lấy điểm ![]() và vẽ các vectơ
và vẽ các vectơ ![]() ,
, ![]() (H.2.10).
(H.2.10).
- Giải thích vì sao
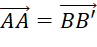 và
và  .
. - Giải thích vì sao
 là hình bình hành, từ đó suy ra
là hình bình hành, từ đó suy ra  .
.

Giải nhanh:
a) ![]() =>
=> ![]() và
và ![]() cùng hướng và cùng độ dài.
cùng hướng và cùng độ dài.
![]() =>
=> ![]() và
và ![]() cùng hướng và cùng độ dài.
cùng hướng và cùng độ dài.
![]() và
và ![]() cùng hướng và cùng độ dài =>
cùng hướng và cùng độ dài => ![]() và
và ![]() .
.
=> ![]() là hình bình hành =>
là hình bình hành => ![]() , hai vectơ
, hai vectơ ![]() và
và ![]() có cùng hướng và cùng độ dài =>
có cùng hướng và cùng độ dài => ![]() .
.
Chứng minh tương tự, ta có ![]() .
.
b) ![]() và
và ![]() cùng hướng và cùng độ dài
cùng hướng và cùng độ dài
![]() và
và ![]() cùng hướng và cùng độ dài
cùng hướng và cùng độ dài
=> ![]() và
và![]() cùng hướng và cùng độ dài =>
cùng hướng và cùng độ dài => ![]() và
và ![]()
=> ![]() là hình bình hành.
là hình bình hành.
=> ![]() và
và ![]() .
.
=> ![]() và
và ![]() có cùng hướng và cùng độ dài =>
có cùng hướng và cùng độ dài => ![]() .
.
Luyện tập 3: Trong Ví dụ 3, hãy tính độ dài của vectơ ![]() .
.
Giải nhanh:
![]() là hình lập phương =>
là hình lập phương => ![]() là hình vuông =>
là hình vuông => ![]() .
.
Ta có: ![]() mà
mà![]()
=>![]()
Luyện tập 4: Cho tứ diện ![]() (H.2.13). Chứng minh rằng
(H.2.13). Chứng minh rằng ![]() .
.
Giải nhanh:
![]()
Hoạt động 4: Thiết lập quy tắc hình hộp.
Cho hình hộp ![]() (H.2.14).
(H.2.14).
- Hai vectơ
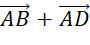 và
và  có bằng nhau hay không?
có bằng nhau hay không? - Hai vectơ
 và
và 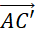 có bằng nhau hay không?
có bằng nhau hay không?

Giải nhanh:
- Vì
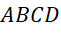 là hình bình hành nên
là hình bình hành nên  .
. - Ta có:
 (1)
(1)
Vì ![]() là hình hộp.
là hình hộp.
=> ![]() và
và ![]() là hình bình hành.
là hình bình hành.
=> ![]() ,
, ![]() và
và ![]() ,
, ![]() .
.
=> ![]() và
và ![]() .
.
=> ![]() là hình bình hành.
là hình bình hành.
=> ![]() (2)
(2)
Từ (1) và (2) =>![]()
Luyện tập 5: Cho hình hộp chữ nhật ![]() . Chứng minh rằng
. Chứng minh rằng ![]() .
.
Giải nhanh:
![]() là hình chữ nhật =>
là hình chữ nhật => ![]() ,
,![]()
![]() là hình hộp chữ nhật =>
là hình hộp chữ nhật =>![]()
![]() .
.
Hoạt động 5: Nhận biết vectơ đối của một vectơ trong không gian.
Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét gì về độ dài và hướng của các vectơ biểu diễn hai lực đó?
Giải nhanh:
Độ dài bằng nhau và hướng ngược nhau.
Luyện tập 6: Trong Ví dụ 6, chứng minh rằng:
 và
và  là hai vectơ đối nhau;
là hai vectơ đối nhau; .
.
Giải nhanh:
a) ![]() là hình bình hành =>
là hình bình hành => ![]() ,
, ![]() .
.
=> ![]() và
và![]()
=> ![]() là hình bình hành
là hình bình hành
=> ![]() và
và ![]() .
.
Hai vectơ ![]() và
và ![]() có cùng độ dài và ngược hướng nên
có cùng độ dài và ngược hướng nên![]() và
và ![]() đối nhau.
đối nhau.
b) Ta có: ![]() =>
=> ![]() .
.
Vận dụng 2: Thang cuốn tại các trung tâm thương mại, siêu thị lớn hay nhà ga, san bay thường có hai làn, trong đó có một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi là có là hai vectơ đối nhau hay không? Giải thích vì sao.
Giải nhanh:
Vectơ biểu diễn vận tốc của mỗi làn có cùng độ lớn và hướng ngược nhau nên chúng là hai vectơ đối nhau.
3. TÍCH CỦA MỘT SỐ VỚI MỘT VECTƠ TRONG KHÔNG GIAN
Hoạt động 6: Hình thành khái niệm tích của một số với một vectơ trong không gian.
Cho hình lăng trụ tam giác ![]() . Gọi
. Gọi ![]() ,
, ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() (H.2.17).
(H.2.17).
- Hai vectơ
 và
và  có cùng phương không? Có cùng hướng không?
có cùng phương không? Có cùng hướng không? - Giải thích vì sao
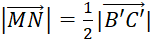 .
.

Giải nhanh:
a) Vì ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]() =>
=> ![]() .
.
Vì ![]() là hình bình hành =>
là hình bình hành => ![]() =>
=> ![]() .
.
=> ![]() và
và ![]() có cùng phương và cùng hướng.
có cùng phương và cùng hướng.
b) Vì ![]() là hình bình hành =>
là hình bình hành => ![]() .
.
Vì ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]() =>
=>
=>
Luyện tập 7: Cho hình chóp ![]() có đáy
có đáy ![]() là hình bình hành. Gọi
là hình bình hành. Gọi ![]() lần lượt là các điểm thuộc các cạnh
lần lượt là các điểm thuộc các cạnh ![]() sao cho
sao cho 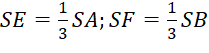 . Chứng minh rằng
. Chứng minh rằng  .
.
Giải nhanh:
Vì  =>
=>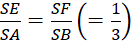
Tam giác ![]() có:
có:  =>
=> ![]() và
và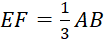
![]() và
và ![]() cùng hướng =>
cùng hướng =>  (1)
(1)
Vì ![]() là hình bình hành =>
là hình bình hành => ![]() và
và ![]() =>
=> ![]() (2)
(2)
Từ (1) và (2) =>  .
.
Luyện tập 8: Trong Ví dụ 8, gọi ![]() là điểm thuộc đoạn thẳng
là điểm thuộc đoạn thẳng ![]() sao cho
sao cho ![]() (H.2.19). Chứng minh rằng:
(H.2.19). Chứng minh rằng:
![]() .
.
Giải nhanh:
![]()
=>![]()
=>![]()
=> ![]() (đpcm)
(đpcm)
Vận dụng 3: Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900 km/h lên 920 km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900 km/h và 920 km/h lần lượt được biểu diễn bởi hai vectơ ![]() và
và ![]() . Hãy giải thích vì sao
. Hãy giải thích vì sao ![]() với
với ![]() là một số thực dương nào đó. Tính giá trị của
là một số thực dương nào đó. Tính giá trị của ![]() (làm tròn kết quả đến chữ số thập phân thứ hai).
(làm tròn kết quả đến chữ số thập phân thứ hai).
Giải nhanh:
Vì trong quá trình tăng vận tốc máy bay giữ nguyên hướng bay => ![]() và
và ![]() có cùng hướng =>
có cùng hướng => ![]() với
với ![]() là một số thực dương nào đó (1).
là một số thực dương nào đó (1).
Gọi ![]() lần lượt là vận tốc của của chiếc máy bay khi đạt 900 km/h và 920 km/h.
lần lượt là vận tốc của của chiếc máy bay khi đạt 900 km/h và 920 km/h.
Vì lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay nên
 =>
=>  (2)
(2)
Từ (1) và (2) =>  =>
=>
4. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ TRONG KHÔNG GIAN
Hoạt động 7: Hình thành khái niệm góc giữa hai vectơ trong không gian.
Trong không gian, cho hai vectơ ![]() khác
khác ![]() . Lấy điểm
. Lấy điểm ![]() và vẽ các vectơ
và vẽ các vectơ ![]() . Lấy điểm
. Lấy điểm ![]() khác
khác ![]() và vẽ các vectơ
và vẽ các vectơ ![]() (H.2.21).
(H.2.21).
- Giải thích vì sao
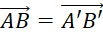 .
. - Áp dụng định lí côsin cho hai tam giác
 và
và  để giải thích vì sao
để giải thích vì sao  .
.
Giải nhanh:
- Ta có:
 ;
;
Mà ![]() =>
=> ![]() ;
; ![]() .
.
=> ![]() .
.
- Áp dụng định lí côsin vào tam giác
 ta có:
ta có: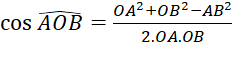
Áp dụng định lí côsin vào tam giác ![]() ta có:
ta có:  .
.
![]() =>
=> ![]() ;
; ![]() =>
=> ![]() ;
; ![]() =>
=>![]()
=> ![]() =>
=> ![]() .
.
Luyện tập 9: Cho hình lăng trụ tam giác đều ![]() (H.2.25). Tính các góc (
(H.2.25). Tính các góc (![]() ) và (
) và (![]() ).
).

Giải nhanh:
Vì ![]() là lăng trụ tam giác đều
là lăng trụ tam giác đều
=> ![]() là hình chữ nhật
là hình chữ nhật
=> ![]() =>
=> ![]() .
.
Vì ![]() là hình chữ nhật =>
là hình chữ nhật =>![]()
=>  .
.
Vì tam giác![]() là tam giác đều nên
là tam giác đều nên ![]() =>
=>![]()
Hoạt động 8: Nhận biết khái niệm tích vô hướng của hai vectơ trong không gian.
Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.
Giải nhanh:
![]()
Luyện tập 10: Trong Ví dụ 10, hãy tính các tích vô hướng ![]() và
và ![]() .
.
Giải nhanh:
Gọi ![]() là giao điểm của hai đường chéo
là giao điểm của hai đường chéo ![]() và
và ![]() trong hình vuông
trong hình vuông ![]() . Do đó,
. Do đó, ![]() là trung điểm của
là trung điểm của ![]() ,
, ![]() là trung điểm của
là trung điểm của ![]() .
.
Tứ giác ![]() là hình vuông cạnh
là hình vuông cạnh ![]() , độ dài đường chéo
, độ dài đường chéo ![]() là
là ![]() =>
=>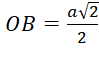
Gọi ![]() là trung điểm của
là trung điểm của ![]() . Mà
. Mà ![]() là trung điểm của
là trung điểm của ![]() nên
nên ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]() =>
=> ![]() và
và  =>
=>![]()
Vì ![]() là trung điểm của
là trung điểm của ![]() nên
nên![]()
Tam giác ![]() có ba cạnh bằng nhau =>
có ba cạnh bằng nhau => ![]() là tam giác đều =>
là tam giác đều => ![]() là đường trung tuyến đồng thời là đường cao của tam giác
là đường trung tuyến đồng thời là đường cao của tam giác ![]() =>
=>
 =>
=> ![]() vuông tại
vuông tại ![]() =>
=>![]()
![]()
![]() là hình vuông =>
là hình vuông =>![]()
Ta có:
![]()
![]()
Vì tam giác ![]() có ba cạnh bằng nhau => tam giác
có ba cạnh bằng nhau => tam giác ![]() đều =>
đều =>![]()
=>
Luyện tập 11: Cho hình lập phương ![]() . Chứng minh rằng
. Chứng minh rằng ![]() .
.
Giải nhanh:
Gọi cạnh của hình lập phương ![]() là
là ![]() =>
=>![]()
Gọi ![]() là giao điểm của hai đường chéo
là giao điểm của hai đường chéo ![]() và
và ![]() của hình vuông
của hình vuông ![]() .
.
=> ![]() là trung điểm của
là trung điểm của ![]() và
và ![]() =>
=> ![]() =>
=>  .
.
Gọi ![]() là trung điểm của
là trung điểm của ![]() . Mà
. Mà ![]() là trung điểm của
là trung điểm của ![]() =>
=> ![]() là đường trung bình của tam giác
là đường trung bình của tam giác ![]() =>
=> ![]() =>
=>  .
.
Áp dụng định lí Pythagore vào ![]() vuông tại
vuông tại ![]() có:
có:
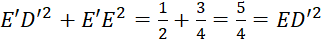 nên
nên ![]() vuông tại
vuông tại ![]() . Do đó
. Do đó![]()
Ta có: ![]() (đpcm)
(đpcm)
Vận dụng 4: Như đã biết, nếu có một lực ![]() tác động vào một vật tại điểm
tác động vào một vật tại điểm ![]() và làm cho vật đó di chuyển một quãng đường
và làm cho vật đó di chuyển một quãng đường ![]() thì công
thì công ![]() sinh ra được tính theo công thức
sinh ra được tính theo công thức ![]() , trong đó lực
, trong đó lực ![]() có độ lớn tính bằng Newton, quãng đường
có độ lớn tính bằng Newton, quãng đường ![]() tính bằng mét và công
tính bằng mét và công ![]() tính bằng Jun (H.2.28). Do đó, nếu dùng một lực
tính bằng Jun (H.2.28). Do đó, nếu dùng một lực ![]() có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao.
có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao.
Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?

Giải nhanh:
![]()
Vì lực ![]() có độ lớn không đổi và vật di chuyển một quãng đường không đổi =>
có độ lớn không đổi và vật di chuyển một quãng đường không đổi => ![]() lớn nhất khi
lớn nhất khi ![]() lớn nhất =>
lớn nhất => ![]() . Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.
. Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.
Khi kéo (hoặc đẩy) các vật nặng, ta nên kéo (hoặc đẩy) cùng cùng hướng với chuyển động của vật.
GIẢI BÀI TẬP
Bài 2.1 trang 58 sách toán 12 tập 1 kntt
Trong không gian, cho ba vectơ ![]() ,
, ![]() ,
, ![]() phân biệt và đều khác
phân biệt và đều khác ![]() . Những mệnh đề nào sau đây là đúng?
. Những mệnh đề nào sau đây là đúng?
- Nếu
 và
và  đều cùng hướng với
đều cùng hướng với  thì
thì  và
và 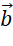 cùng hướng.
cùng hướng. - Nếu
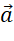 và
và  đều ngược hướng với
đều ngược hướng với  thì
thì  và
và  cùng hướng.
cùng hướng. - Nếu
 và
và  đều cùng hướng với
đều cùng hướng với  thì
thì 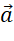 và
và  ngược hướng.
ngược hướng. - Nếu
 và
và  đều ngược hướng với
đều ngược hướng với  thì
thì  và
và 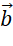 ngược hướng.
ngược hướng.
Giải nhanh:
a, b.
Bài 2.2 trang 58 sách toán 12 tập 1 kntt
Cho hình hộp chữ nhật ![]() có
có ![]() và
và ![]() . Tính độ dài của các vectơ
. Tính độ dài của các vectơ ![]() và
và ![]() .
.
Giải nhanh:
Vì ![]() là hình chữ nhật =>
là hình chữ nhật => ![]() =>
=>![]()
Vì ![]() là hình chữ nhật => tam giác
là hình chữ nhật => tam giác ![]() vuông tại
vuông tại ![]() .
.
Do đó, ![]() (định lý Pythagore)
(định lý Pythagore)
=> ![]() .
.
Vì ![]() là hình chữ nhật =>
là hình chữ nhật => ![]() vuông tại
vuông tại ![]() .
.
Theo định lí Pythagore ta có:
![]() =>
=>
Bài 2.3 trang 58 sách toán 12 tập 1 kntt
Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt bàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ ![]() ) phân tác đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ
) phân tác đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ ![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
- Hãy chỉ ra mỗi quan hệ về phương và hướng của các vectơ
 và
và  .
. - Giải thích vì sao các vectơ
 đôi một bằng nhau.
đôi một bằng nhau.
Giải nhanh:
- Các vectơ
 và
và  có cùng phương; các vectơ
có cùng phương; các vectơ  cùng hướng với nhau và ngược hướng với vectơ
cùng hướng với nhau và ngược hướng với vectơ  .
. - Vì trọng lực tác dụng lên bàn phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn nên các vectơ
 có độ lớn bằng nhau. Mà các vectơ
có độ lớn bằng nhau. Mà các vectơ  cùng hướng với nhau. Do đó, các vectơ
cùng hướng với nhau. Do đó, các vectơ  đôi một bằng nhau.
đôi một bằng nhau.
Bài 2.4 trang 58 sách toán 12 tập 1 kntt
Cho hình hộp ![]() . Chứng minh rằng:
. Chứng minh rằng:
 ;
; ;
;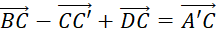 .
.
Giải nhanh:
- Vì
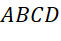 là hình bình hành =>
là hình bình hành =>  .
.
Vì ![]() là hình bình hành =>
là hình bình hành => ![]() ,
,![]()
Ta có:  .
.
- Ta có:

- Vì
 là hình bình hành =>
là hình bình hành =>
Vì ![]() là hình bình hành =>
là hình bình hành =>![]()

Bài 2.5 trang 58 sách toán 12 tập 1 kntt
Cho hình lăng trụ tam giác ![]() có
có ![]() và
và ![]() . Hãy biểu diễn các vectơ sau qua các vectơ
. Hãy biểu diễn các vectơ sau qua các vectơ ![]() :
:
 ;
;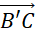 ;
; .
.
Giải nhanh:
- Vì
 là hình bình hành =>
là hình bình hành =>  .
. - Vì
 là hình bình hành =>
là hình bình hành =>  .
.
Ta có:![]()
Vì ![]() là hình bình hành nên:
là hình bình hành nên:
![]() =>
=>![]()
- Vì
 là hình bình hành =>
là hình bình hành =>
Bài 2.6 trang 58 sách toán 12 tập 1 kntt
Cho hình chóp tứ giác ![]() . Chứng minh rằng tứ giác
. Chứng minh rằng tứ giác ![]() là hình bình hành nếu và chỉ nếu
là hình bình hành nếu và chỉ nếu ![]() .
.
Giải nhanh:
Gọi ![]() là tâm hình bình hành
là tâm hình bình hành ![]() =>
=> ![]() là trung điểm của
là trung điểm của ![]() .
.
=>![]()
Ta có:![]()
![]()
Do đó: ![]()
Ta có:![]()
=> ![]() và
và ![]() cùng hướng và có độ lớn bằng nhau.
cùng hướng và có độ lớn bằng nhau.
=> ![]() =>
=> ![]() là hình bình hành.
là hình bình hành.
Bài 2.7 trang 58 sách toán 12 tập 1 kntt
Cho hình chóp ![]() . Trên cạnh
. Trên cạnh ![]() , lấy điểm
, lấy điểm ![]() sao cho
sao cho ![]() . Trên cạnh
. Trên cạnh ![]() , lấy điểm
, lấy điểm ![]() sao cho
sao cho ![]() . Chứng minh rằng
. Chứng minh rằng  .
.
Giải nhanh:
Ta có:
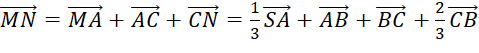
 (đpcm)
(đpcm)
Bài 2.8 trang 58 sách toán 12 tập 1 kntt
Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ![]() là một điểm
là một điểm ![]() thỏa mãn
thỏa mãn ![]() , ở đó
, ở đó ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() . Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).
. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm (H.2.30).
Giải nhanh:
Đặt tên khối rubik là tứ diện đều ![]() có
có ![]() là trọng tâm của tam giác
là trọng tâm của tam giác ![]() ,
, ![]() là trọng tâm của tứ diện
là trọng tâm của tứ diện![]()
=> ![]() =>
=>
Vì chiều cao của rubik bằng 8 cm => ![]() cm =>
cm => 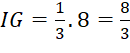 (cm)
(cm)
Vậy khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó bằng ![]() cm.
cm.
Bài 2.9 trang 59 sách toán 12 tập 1 kntt
Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao.
Giải nhanh:
Ta có cách đặt ba sợi dây theo vectơ dưới đây:

Lấy điểm ![]() sao cho tứ giác
sao cho tứ giác ![]() là hình bình hành (điểm
là hình bình hành (điểm ![]() nằm khác phía với điểm
nằm khác phía với điểm ![]() ).
).
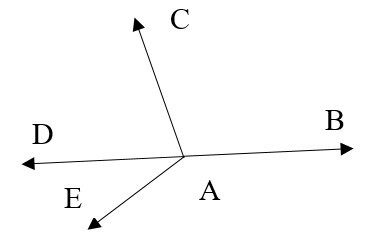
Do đó, giá của các vectơ ![]() và
và ![]() cùng nằm trên mặt phẳng
cùng nằm trên mặt phẳng ![]() . (1)
. (1)
Vì ![]() là hình bình hành nên
là hình bình hành nên![]()
Vì các lực kéo làm cho ba sợi dây ở trạng thái đứng yên nên ![]() , do đó hai vectơ
, do đó hai vectơ![]() và
và ![]() có giá cùng nằm trên mặt phẳng
có giá cùng nằm trên mặt phẳng ![]() . (2)
. (2)
Từ (1) và (2) suy ra ba vectơ ![]() và
và ![]() có giá cùng nằm trên mặt phẳng
có giá cùng nằm trên mặt phẳng ![]() .
.
Vậy khi các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng.
Bài 2.10 trang 59 sách toán 12 tập 1 kntt
Cho hình lăng trụ tứ giác đều ![]() có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:
có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:
 ;
;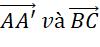 ;
; .
.
Giải nhanh:
- Vì
 =>
=> 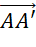 và
và 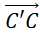 ngược hướng nhau.
ngược hướng nhau.
=>![]()
 .
.
- Vì
 là hình chữ nhật =>
là hình chữ nhật =>
Vì ![]() là hình vuông =>
là hình vuông => ![]() .
.
=> ![]()
![]()
- Vì
 là hình chữ nhật =>
là hình chữ nhật =>  .
.
Vì ![]() là hình vuông =>
là hình vuông => ![]() và
và![]()

Bài 2.11 trang 59 sách toán 12 tập 1 kntt
Trong không gian, cho hai vectơ ![]() và
và ![]() cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là 45o, hãy tính:
cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là 45o, hãy tính:
 ;
;- (
 ;
;  .
.
Giải nhanh:
Bài 2.12 trang 59 sách toán 12 tập 1 kntt
Cho tứ diện ![]() . Chứng minh rằng:
. Chứng minh rằng:
 ;
;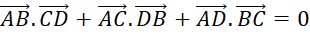 .
.
Giải nhanh:
![]()
![]()
![]()
![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều




Bình luận