BÀI 18: XÁC SUẤT CÓ ĐIỀU KIỆN

1. Xác suất có điều kiện

Hoạt động 1: Hình thành khái niệm xác suất có điều kiện

Trong một hộp kín có 7 chiếc bút bi xanh và 5 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi trong hộp, không trả lại. Sau đó Tùng lấy ngẫu nhiên một trong 11 chiếc bút còn lại. Tính xác suất để Tùng lấy được bút bi xanh nếu biết rằng Sơn đã lấy được bút bi đen.

Giải nhanh:

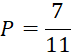
Luyện tập 1: Trở lại Ví dụ 1. Tính bằng định nghĩa và bằng công thức.

Giải nhanh:

A: ”An lấy được viên bi trắng”

B: ”Bình lấy được viên bi trắng”

: ”Bình lấy được viên bi đen”

Cách 1: Bằng định nghĩa

Nếu xảy ra tức là Bình lấy được viên bi đen. Khi đó, trong hộp còn lại 29 viên bi với 20 viên bi trắng và 9 viên bi đen =>

Cách 2: Bằng công thức

Bình có 30 cách chọn, An có 29 cách chọn một viên bi trong hộp

=>

Bình có 10 cách chọn một viên bi đen, An có 29 cách chọn từ 29 viên bi còn lại

=> và  

Bình có 10 cách chọn một viên bi đen, An có 20 cách chọn một viên bi trắng

=> và  

Như vậy

Luyện tập 2: Chứng tỏ rằng nếu và là hai biến cố độc lập thì:

và .

Giải nhanh:

• Theo định nghĩa, 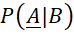là xác suất của 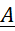, tính trong điều kiện biết rằng biến cố B đã xảy ra

Nếu A và B là 2 biến cố độc lập thì và B cũng độc lập. Vì vậy, việc xảy ra B không ảnh hưởng tới xác suất hiện của =>

• Theo định nghĩa, 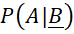là xác suất của 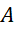, tính trong điều kiện biết rằng biến cố 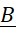đã xảy ra

Nếu A và B là 2 biến cố độc lập thì A và cũng độc lập. Vì vậy, việc xảy ra không ảnh hưởng tới xác suất hiện của A =>

Luyện tập 3: Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N. Công ty đã thử tiến hành thử nghiệm với 4000 bệnh nhân mắc bệnh X trong đó 2400 bệnh nhân dùng thuốc M, 1600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong bảng dữ liệu thống kê 2 x 2 như sau:

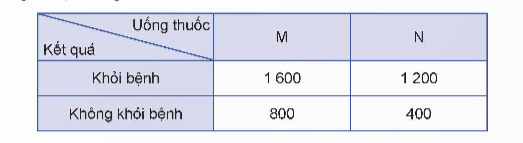
Chọn ngẫu nhiên một bệnh nhân trong số 4000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó

a) uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh;

b) uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.

Giải nhanh:

Không gian mẫu là tập hợp gồm 4000 bệnh nhân mắc bệnh X ⇒

a) Gọi A là biến cố:”Người đó uống thuốc M”; B là biến cố:”Người đó khỏi bệnh”

Khi đó AB là biến cố:”Người đó uống thuốc M và khỏi bệnh”

Ta cần tính

Số người khỏi bệnh là: 1600 + 1200 = 2800 ⇒

=> 

Trong số những người khỏi bệnh, có 1600 người uống thuốc M ⇒

=> 

=>

b) là biến cố:”Người đó uống thuốc N”

là biến cố:”Người đó không qua khỏi”

Khi đó là biến cố:”Người đó uống thuốc N và không khỏi bệnh”

Ta cần tính

Số người không khỏi bệnh là 800 + 400 = 1200 ⇒

=> 

Trong số những người không khỏi bệnh, có 400 người uống thuốc M 

⇒

=> 

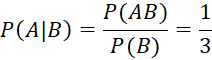
2. Công thức nhân xác suất

Hoạt động 2: Hình thành công thức nhân xác suất

Chứng minh rằng, với hai biến cố A và B, > 0 , ta có:

Giải nhanh:

(đpcm)

Luyện tập 4: Trở lại Ví dụ 4. Tính xác suất để:

a) Sơn lấy được bút bi xanh và Tùng lấy được bút bi đen;

b) Hai chiếc bút lấy ra có cùng màu.

Giải nhanh:

a) Dựa vào sơ đồ hình cây

Trên nhánh XĐ tương ứng ghi xác suất lấy được bút đen với điều kiện đã lấy được bút xanh

Vậy xác suất cần tính là:

b) Trên nhánh ĐĐ, XX tương ứng ghi xác suất lấy được 2 bút đen và 2 bút xanh

Vậy xác suất cần tính là:

Vận dụng: Trở lại trò chơi “Ô cửa bí mật” trong tình huống mở đầu. Giả sử người chơi chọn cửa số 1 và người quản trò mở cửa số 3.

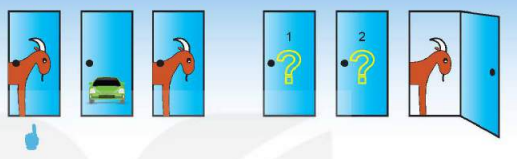
Kí hiệu tương ứng là các biến cố: “Sau ô cửa số 1 có ô tô”; “Sau ô cửa số 2 có ô tô”; “Sau ô cửa số 3 có ô tô” và là biến cố: “Người quản trò mở ô cửa số 3 thấy con lừa”.

Sau khi người quản trò mở cánh cửa số 3 thấy con lừa, tức là khi xảy ra. Để quyết định thay đổi lựa chọn hay không, người chơi cần so sánh hai xác suất có điều kiện: và .

a) Chứng minh rằng:

• ;

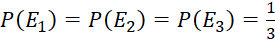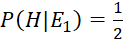• và .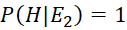

b) Sử dụng công thức tính xác suất có điều kiện và công thức nhân xác suất, chứng minh rằng:

• ;

• .

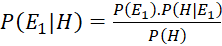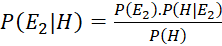c) Từ các kết quả trên hãy suy ra:

Từ đó hãy đưa ra lời khuyên cho người chơi: Nên giữ nguyên lựa chọn ban đầu hay chuyển sang cửa chưa mở còn lại?

Giải nhanh:

a) Vì chỉ có một chiếc ô tô ở đằng sau cả 3 cánh cửa nên:

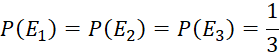
Nếu xảy ra, tức là sau cửa sổ 1 có ô tô. Khi đó, sau cửa số 2 và 3 là con lừa. Người quản trò chọn ngẫu nhiên một trong hai cửa số 2 và 3 để mở ra. Do đó, việc chọn cửa số 2 hay cửa số 3 có khả năng như nhau. Vậy

Nếu xảy ra, tức là cửa số 2 có ô tô. Khi đó, người quản trò chắc chắn phải mở cửa số 3. Do đó

b) Theo công thức nhân xác suất: 

Tương tự:

c) Từ câu b, ta có:

Từ câu a, ta có: ; và

Vậy

Lời khuyên: Người chơi là nên chuyển sang cửa chưa mở còn lại.

GIẢI BÀI TẬP

Bài 6.1 trang 70 sách toán 12 tập 2 kntt

Một hộp kín đựng 20 tấm thẻ giống hệt nhau đánh số từ 1 đến 20. Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ số 10.

Giải nhanh:

Gọi A là biến cố:”Người đó rút được thẻ mang số chẵn”

B là biến cố:”Người đó rút được thẻ số 10”

và là hai biến cố độc lập nên  =

Bài 6.2 trang 70 sách toán 12 tập 2 kntt

Cho . Tính .

Giải nhanh:

Ta có: 

=>

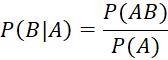
Bài 6.3 trang 70 sách toán 12 tập 2 kntt

Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để:

a) Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 nếu biết rằng ít nhất có một con xúc xắc xuất hiện mặt 5 chấm.

b) Có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm nếu biết rằng tổng số chấm xuất hiện trên hai con xúc xắc bằng 7.

Giải nhanh:

Gieo hai con xúc xắc cân đối, đồng chất nên số phần tử của không gian mẫu là:

Gọi A là biến cố:”Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7”

B là biến cố:”Có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm”

Khi đó AB là biến cố:”Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 và có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm”

Các kết quả thuận lợi cho biến cố A là: (1;6), (2;5), (3;4), (4;3), (5;2), (6;1)

⇒ ⇒

Các kết quả thuận lợi cho biến cố B là: (1;5), (2;5), (3;5), (4;5), (5;5), (6;5), (5;1), (5;2), (5;3), (5;4), (5;6)

⇒ ⇒

Các kết quả thuận lợi cho biến cố AB là: (2;5), (5;2)

⇒ ⇒

a)

b)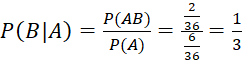

Bài 6.4 trang 70 sách toán 12 tập 2 kntt

Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10 nếu biết rằng có ít nhất một con xúc xắc xuất hiện mặt 5 chấm.

Giải nhanh:

Gieo hai con xúc xắc cân đối, đồng chất nên số phần tử của không gian mẫu là:

Gọi A là biến cố:”Tổng số chấm xuất hiện trên hai con xúc xắc không nhỏ hơn 10”

B là biến cố:”Có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm”

Khi đó AB là biến cố:”Tổng số chấm xuất hiện trên hai con xúc xắc không nhỏ hơn 10 và có ít nhất có một con xúc xắc xuất hiện mặt 5 chấm”

Các kết quả thuận lợi cho biến cố B là: (1;5), (2;5), (3;5), (4;5), (5;5), (6;5), (5;1), (5;2), (5;3), (5;4), (5;6)

⇒ ⇒

Các kết quả thuận lợi cho biến cố AB là: (5;5), (5;6), (6;5)

⇒ ⇒

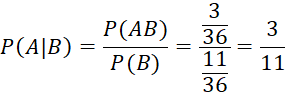
Bài 6.5 trang 70 sách toán 12 tập 2 kntt

Bạn An phải thực hiện hai thí nghiệm liên tiếp. Thí nghiệm thứ nhất có xác suất thành công là 0,7. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,9. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai chỉ là 0,4. Tính xác suất để:

a) Cả hai thí nghiệm đều thành công;

b) Cả hai thí nghiệm đều không thành công;

c) Thí nghiệm thứ nhất thành công và thí nghiệm thứ hai không thành công.

Giải nhanh:

Gọi A là biến cố:”Thí nghiệm thứ nhất thành công”

B là biến cố:”Thí nghiệm thứ hai thành công”

Khi đó AB là biến cố:”Thí nghiệm thứ hai thành công”

Ta có: )= 0,4

a)

b) là biến cố:”Cả hai thí nghiệm đều không thành công”

c)  là biến cố:”Thí nghiệm thứ nhất thành công và thí nghiệm thứ hai không thành công”

Bài 6.6 trang 70 sách toán 12 tập 2 kntt

Trong một túi có một số chiếc kẹo cùng loại, chỉ khác màu, trong đó có 6 cái kẹo màu cam, còn lại là kẹo màu vàng. Hà lấy ngẫu nhiên một cái kẹo từ trong túi, không trả lại. Sau đó Hà lại lấy ngẫu nhiên thêm một cái kẹo khác từ trong túi. Biết rằng xác suất Hà lấy được cả hai cái kẹo màu cam là . Hỏi ban đầu trong túi có bao nhiêu cái kẹo?

Giải nhanh:

Gọi A là biến cố:”Lấy được cái kẹo thứ nhất màu cam”

B là biến cố:”Lấy được cái kẹo thứ hai màu cam”

Khi đó AB là biến cố:”Lấy được cả hai cái kẹo màu cam”,

Gọi số kẹo ban đầu có trong túi là n (n > 0)

Như vậy, trong túi có 6 cái kẹo màu cam và cái kẹo màu vàng

Có n cách chọn cái kẹo thứ nhất và cách chọn cái kẹo thứ hai

⇒

Sau khi Hà lấy được 1 cái kẹo màu cam thì còn lại cái kẹo với 5 cái kẹo màu cam

⇒ và

Ta có:

Hay

⇒ hoặc

Như vậy ban đầu trong túi có 10 cái kẹo