BÀI 19: CÔNG THỨC XÁC SUẤT TOÀN PHẦN VÀ CÔNG THỨC BAYES

1. Công thức xác suất toàn phần

Hoạt động 1. Hình thành công thức xác suất toàn phần

Gọi là biến cố “Trời mưa” và là biến cố “Bán hết vé” trong tình huống mở đầu.

Số khán giả đến xem buổi biểu diễn ca nhạc ngoài trời phụ thuộc vào thời tiết. Giả sử, nếu trời không mưa thì xác suất để bán hết vé là 0,9; còn nếu trời mưa thì xác suất để bán hết vé chỉ là 0,4. Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là 0,75. Nhà tổ chức sự kiện quan tâm đến xác suất để bán được hết vé là bao nhiêu.

a) Tính

b) Trong hai xác suất P(A) và P(B), nhà tổ chức sự kiện quan tâm đến xác suất nào nhất? 

Giải nhanh:

a)

b) Nhà tổ chức sự kiện quan tâm đến xác suất để bán được hết vé là bao nhiêu nhất, tức P(B)

Luyện tập 1. Trở lại tình huống mở đầu Mục 1. Tính xác suất để nhà tổ chức sự kiện bán hết vé

Giải nhanh:

Luyện tập 2. Trở lại ví dụ 1. Sử dụng sơ đồ hình cây, hãy mô tả cách tính xác suất để thứ Tư, ông An đi làm bằng xe buýt.

Giải nhanh:

A là biến cố: “Thứ Ba, ông An đi làm bằng xe máy”; B là biến cố: “Thứ Tư, ông An đi làm bằng xe máy”

Khi đó là biến cố: “Thứ Ba, ông An đi làm bằng xe buýt”; là biến cố: “Thứ Tư, ông An đi làm bằng xe buýt

Có 2 nhánh cây đi tới là và

=>

Luyện tập 3. Với giả thiết như vận dụng trên.

a) Hãy ước lượng tỉ lệ cây con có kiểu gen BB.

b) Sử dụng kết quả của vận dụng trên và câu a, hãy ước lượng tỉ lệ cây con có kiểu gen Bb.

Giải nhanh:

a) 

Gọi A là biến cố: “Cây bố có kiểu gen Bb”;

M là biến cố: “Cây con lấy gen B từ cây bố”; 

N là biến cố: “Cây con lấy gen B từ cây mẹ”; 

E là biến cố: “Cây con có kiểu gen BB”.

Theo giả thiết, M và N độc lập nên

Áp dụng công thức xác suất toàn phần:

(*)

Ta có:  

là xác suất để cây con lấy gen B từ cây bố với điều kiện cây bố có kiểu gen Bb.

Do đó

là xác suất để cây con lấy gen B từ cây bố với điều kiện cây bố có kiểu gen bb.

Do đó

Thay vào (*) ta được:

Tương tự tính được

=>

b) Tỉ lệ cây con có kiểu gen Bb là:

2. Công thức Bayes

Hoạt động 2. Phân biệt và

Trong tình huống mở đầu Mục 2, gọi A là biến cố: “Ông M mắc bệnh hiểm nghèo X”; B là biến cố: “Xét nghiệm cho kết quả dương tính”.

a) Nêu các nội dung còn thiếu tương ứng với “(?)” để hoàn thành các câu sau đây:

là xác suất để (?) với điều kiện (?);

là xác suất để (?) với điều kiện (?).

b) 0,95 là hay ? Có phải ông M có xác suất 0,95 mắc bệnh hiểm nghèo X không?

Giải nhanh:

a) là xác suất để ông M mắc bệnh hiểm nghèo X với điều kiện xét nghiệm cho kết quả dương tính

là xác suất để xét nghiệm cho kết quả dương tính với điều kiện ông M mắc bệnh hiểm nghèo X

b) 0,95 là

Không phải ông M có xác suất 0,95 mắc bệnh hiểm nghèo X

Luyện tập 4. 

Trong một kho rượu có 30% là rượu loại I. Chọn ngẫu nhiên một chai rượu đưa cho ông Tùng, một người sành rượu, để nếm thử. Biết rằng, một chai rượu loại I có xác suất 0,9 để ông Tùng xác nhận là loại I; một chai rượu không phải loại I có xác suất 0,95 để ông Tùng xác nhận đây không phải là loại I. Sau khi nếm, ông Tùng xác nhận đây là rượu loại I. Tính xác suất để chai rượu đúng là rượu loại I.

Giải nhanh:

Gọi A là biến cố:”Chai rượu đúng là rượu loại I”;

B là biến cố:”Ông Tùng xác nhận đây là rượu loại I”

Theo công thức Bayes, ta cần biết:

Ta có:

là xác suất để một chai rượu mà ông Tùng xác nhận là loại I với điều kiện đây đúng là rượu loại I

là xác suất để một chai rượu mà ông Tùng xác nhận không phải là loại I với điều kiện đây không phải loại rượu loại I

Thay vào công thức Bayes ta có:

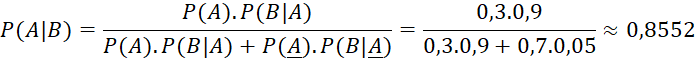
Luyện tập 5.

Trở lại tình huống mở đầu Mục 2. Thống kê cho thấy tỉ lệ dân số mắc bệnh hiểm

nghèo X là 0,2%.

a) Trước khi tiến hành xét nghiệm, xác suất mắc bệnh hiểm nghèo X của ông M là bao nhiêu?

b) Sau khi xét nghiệm cho kết quả dương tính, xác suất mắc bệnh hiểm nghèo X của ông M là bao nhiêu?

Giải nhanh:

a) Xác suất mắc bệnh hiểm nghèo X của ông M là 0,002

b)

Với p là tỉ lệ dân số mắc bệnh hiểm nghèo x

Với ta có:

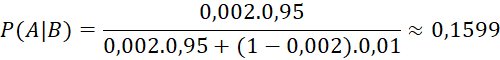
Sau khi xét nghiệm cho kết quả dương tính, xác suất mắc bệnh hiểm nghèo X của ông M là 0,1599

GIẢI BÀI TẬP

Bài 6.7 trang 70 sách toán 12 tập 2 kntt

Trong quân sự, một máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X với xác suất 0,55. Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.

Xét phương án tác chiến sau: Nếu máy bay xuất hiện tại X thì bắn 2 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn 1 quả tên lửa.

Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 1 quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên.

Giải nhanh:

Gọi A là biến cố:”Máy bay chiến đấu của đối phương xuất hiện tại X”

B là biến cố:”Máy bay chiến đấu của đối phương bị bắn hạ”

Ta cần tính

Theo công thức xác suất toàn phần, ta có:

là xác suất máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X

là xác suất máy bay chiến đấu của đối phương bị bắn hạ với điều kiện là nó xuất hiện ở vị trí X

Mà nếu máy bay xuất hiện tại X thì bắn 2 quả tên lửa, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và máy bay bị bắn hạ nếu nó trúng ít nhất 1 quả tên lửa

là xác suất máy bay chiến đấu của đối phương bị bắn hạ với điều kiện là nó xuất hiện ở vị trí Y

Vậy xác suất bắn hạ máy bay đối phương trong phương án tác chiến trên là 0,888

Bài 6.8 trang 70 sách toán 12 tập 2 kntt

Có hai chuồng thỏ. Chuồng I có 5 con thỏ đen và 10 con thỏ trắng. Chuồng II có 7 con thỏ đen và 3 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 1 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 1 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.

Giải nhanh:

Gọi A là biến cố:”Con thỏ lấy ra từ chuồng II là con thỏ trắng”

B là biến cố:”Con thỏ lấy ra từ chuồng I là con thỏ trắng”

Ta cần tính

Theo công thức xác suất toàn phần, ta có:

Chuồng II có 7 con thỏ đen và 3 con thỏ trắng nên:

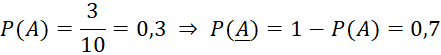
là xác suất con thỏ lấy ra từ chuồng I là con thỏ trắng với điều kiện con thỏ lấy ra từ chuồng II là con thỏ trắng, khi đó chuồng I có 5 con thỏ đen và 11 con thỏ trắng

là xác suất con thỏ lấy ra từ chuồng I là con thỏ trắng với điều kiện con thỏ lấy ra từ chuồng II là con thỏ đen, khi đó chuồng I có 6 con thỏ đen và 10 con thỏ trắng

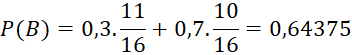
Vậy xác suất để con thỏ được lấy ra từ chuồng I là con thỏ trắng là 0,64375

Bài 6.8 trang 70 sách toán 12 tập 2 kntt

Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK; nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường.

a) Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.

b) Dùng sơ đồ hình cây, hãy mô tả cách tính xác suất để linh kiện điện tử được chọn không được đóng dấu OTK.

Giải nhanh:

Gọi A là biến cố:”Một linh kiện điện tử đạt tiêu chuẩn”

B là biến cố:”Một linh kiện được đóng dấu OTK”

Theo công thức xác suất toàn phần, ta có:

Tỉ lệ sản phẩm đạt tiêu chuẩn là 80%

là xác suất một linh kiện được đóng dấu OTK với điều kiện nó đạt tiêu chuẩn

là xác suất một linh kiện không được đóng dấu OTK với điều kiện nó không đạt tiêu chuẩn

Vậy xác suất để linh kiện điện tử đó được đóng dấu OTK là 0,802

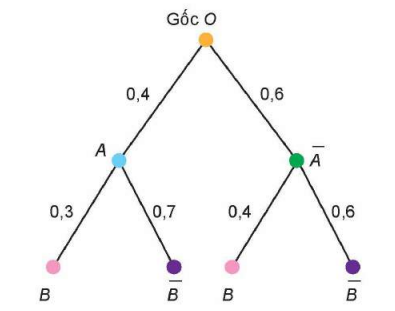
b) Sơ đồ hình cây:

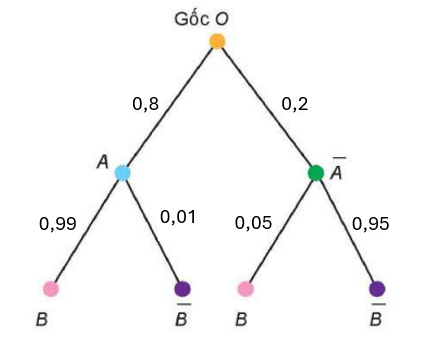
Có 2 nhánh cây đi tới là  

Vậy xác suất để linh kiện điện tử được chọn không được đóng dấu OTK là:

Bài 6.10 trang 70 sách toán 12 tập 2 kntt

Có hai đội thi đấu môn Bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên.

a) Tính xác suất để vận động viên này đạt huy chương vàng;

b) Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

Giải nhanh:

a) Gọi A là biến cố:”Vận động viên thuộc đội I”

B là biến cố:”Vận động viên đạt huy chương vàng”

Theo công thức xác suất toàn phần, ta có:

Đội I có 5 vận động viên, đội II có 7 vận động viên nên: 

và

là xác suất để vận động viên đạt huy chương vàng với điều kiện vận động viên này thuốc đội I nên

là xác suất để vận động viên đạt huy chương vàng với điều kiện vận động viên này thuốc đội I nên

Thay vào công thức ta có:

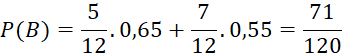
b) Theo công thức Bayes ta có:

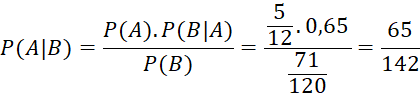
Như vậy xác suất để vận động viên này thuộc đội I là

Bài 6.11 trang 70 sách toán 12 tập 2 kntt

Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3%

a) Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác.

b) Chọn ngẫu nhiên một thư không bị chặn. Tính xác suất để đó là thư đúng.

c) Trong số các thư bị chặn, có bao nhiêu phần trăm là thư đúng? Trong số các thư không bị chặn, có bao nhiêu phần trăm là thư rác?

Giải nhanh:

Gọi A là biến cố: “Thư bị chặn”

B là biến cố: “Thư đó là thư rác”

Vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01 nên:

và

Tỉ lệ thư rác là 3% nên:  

a) Theo công thức Bayes ta có:

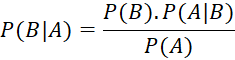
Theo công thức xác suất toàn phần, ta có:

Hay

Thay vào công thức ta có:

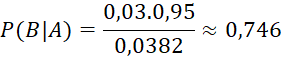
Vây xác suất để thư bị chặn là thư rác là 0,746 

b) Theo công thức Bayes ta có:

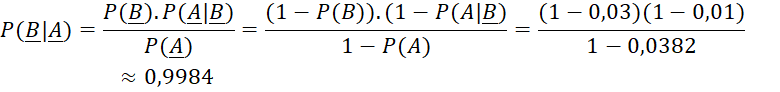
Vậy xác suất để thư không bị chặn là thư đúng là 0,9984

c)

Vậy trong số các thư bị chặn, có 25,39% là thư đúng

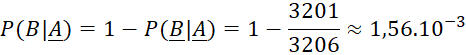
Vậy trong số các thư không bị chặn, có 0,156% là thư rác