TRẮC NGHIỆM

Giả sử tỉ lệ người dân của tỉnh Khánh Hòa nghiện thuốc lá là 20%, tỉ lệ người bị bệnh phổi trong số người nghiện thuốc lá là 70%, trong số người không nghiện thuốc lá là 15%.

Câu 1: Hỏi khi ta gặp ngẫu nhiên một người dân của tỉnh Khánh Hòa thì khả năng mà người đó bị bệnh phổi là bao nhiêu?

• A. 15%.
• B. 29%.
• C. 31%.

• D. 26%

Câu 2: Tính xác suất mà người đó là người nghiện thuốc là khi biết bị bệnh phổi.

• A. .

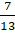• B. .
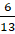• C. .
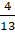• D. .

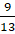Câu 3: Tính .

• A. .

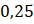• B. .

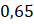• C. .
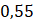• D. .

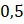Câu 4: Tính .

• A. .
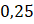• B. .

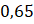• C. .

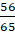• D. .

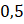Câu 5: Một căn bệnh có 1% dân số mắc phải. Một phương pháp chuẩn đoán được phát triển có tỷ lệ chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 99 trong 100 trường hợp. Nếu một người kiểm tra và kết quả là dương tính, xác suất để người đó thực sự bị bệnh là bao nhiêu?

• A. 0,4
• B. 0,35

• C. 0,5

• D. 0,65

Câu 6: Một chiếc hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số viên bi màu đỏ đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số. Lấy ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra được đánh số là:

• A. .

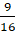• B. .
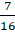• C. .
• D. .

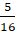Câu 7: Trong một lớp học, có hai nhóm học sinh A và B. Xác suất chọn một học sinh từ nhóm A là 0,4 và từ nhóm B là 0,6. Xác suất của việc một học sinh thuộc nhóm A làm bài kiểm tra là 0,5 và xác suất của việc một học sinh thuộc nhóm B làm bài kiểm tra là 0,7. Tính xác suất tổng quát để một học sinh được chọn ngẫu nhiên từ lớp học làm bài kiểm tra.

• A. 0,58.

• B. 0,62.

• C. 0,65.
• D. 0,7.

Trong một trường học, tỉ lệ học sinh nữ là 52%. Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là 18% và 15%. Gặp ngẫu nhiên 1 học sinh của trường.

Câu 8: Cho hai biến cố và với . Phát biểu nào sau đây là đúng?

• A. .
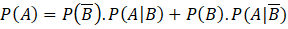• B. .
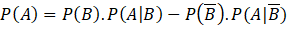• C. .

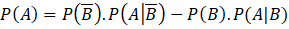• D. .

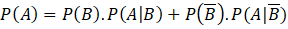Câu 9: Cho hai biến cố có xác suất . Khi đó, bằng:

• A. .

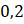• B.
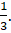
• C.
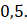
• D. .

Câu 10: Cho các biến cố và thỏa mãn . Khi đó, bằng biểu thức nào dưới đây?

• A. .

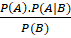• B. .
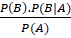• C. .
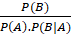• D. .

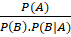Câu 11: Cho hai biến cố và , với các xác suất sau: . Tính xác suất .

• A. 0,5.

• B. 0,6.

• C. 0,7.
• D. 0,8.

Câu 12: Trong một trường học có 3 khối 10; 11 và 12. Tỉ lệ học sinh trong các khối lần lượt là 30%, 40% và 30%. Trong số học sinh của mỗi khối, tỉ lệ học sinh đạt học sinh giỏi trong mỗi kì lần lượt là 50%, 60% và 40%. Chọn ngẫu nhiên một học sinh từ trường đó biết học sinh đó đạt học sinh giỏi, tính xác suất để học sinh đó thuộc vào khối 10.

• A. 0,51.
• B. .
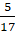• C.
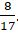
• D. .

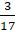Câu 13: Một công ty có 3 loại sản phẩm: Sản phẩm X, Sản phẩm Y, và Sản phẩm Z. Tỉ lệ các sản phẩm trong công ty là:

• Sản phẩm X: 20%
• Sản phẩm Y: 50%
• Sản phẩm Z: 30%

Xác suất một sản phẩm X bị lỗi là 5%, xác suất một sản phẩm Y bị lỗi là 10%, và xác suất một sản phẩm Z bị lỗi là 15%.

Một sản phẩm được chọn ngẫu nhiên từ công ty và được phát hiện là bị lỗi. Tính xác suất để sản phẩm đó là Sản phẩm Y.

• A. 0,45

• B. 0,5

• C. 0,55
• D. 0,6

Câu 14: Một loại linh kiện do hai nhà máy số I, số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: 4%; 3%. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số I và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó. Tính xác suất để linh kiện được lấy ra là linh kiện tốt.

• A. 0,034.

• B. 0,966.

• C. 0,736.
• D. 0,751.

Câu 15: Tỉ lệ người dân đã tiêm vắc xin phòng bệnh A ở một địa phương là 65%. Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh A là 5% còn trong số những người chưa tiêm, tỉ lệ mắc bệnh A là 17%. Gặp ngẫu nhiên một người ở địa phương đó. Biết rằng người đó mắc bệnh A. Tính xác suất người đó không tiệm vắc xin phòng bệnh A.

• A. 0,646

• B. 0,5
• C. 0,36
• D. 0,484.