Dễ hiểu giải Toán 12 Kết nối bài 15: Phương trình đường thẳng trong không gian
Giải dễ hiểu bài 15: Phương trình đường thẳng trong không gian. Trình bày rất dễ hiểu, nên tiếp thu Toán 12 Kết nối dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 15: PHƯƠNG TRÌNH ĐƯỜNG THẲNG TRONG KHÔNG GIAN
1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
a) Vecto chỉ phương của đường thẳng
Hoạt động 1. Hình thành khái niệm vectơ chỉ phương của đường thẳng
Trong không gian, cho điểm M và vectơ ![]() khác vectơ – không. Khẳng định nào trong hai khẳng định sau là đúng?
khác vectơ – không. Khẳng định nào trong hai khẳng định sau là đúng?
a) Có duy nhất đường thẳng đi qua M và vuông góc với giá của ![]() .
.
b) Có duy nhất đường thẳng đi qua M và song song hoặc trùng với giá của ![]() .
.
Giải nhanh:
Khẳng định b đúng
Luyện tập 1.
Cho hình lăng trụ ![]() (H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng
(H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng ![]() ?
?
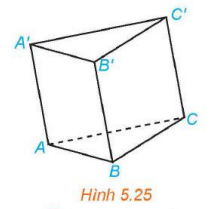
Giải nhanh:
![]()
b) Phương trình tham số của đường thẳng
Hoạt động 2. Hình thành khái niệm phương trình tham số của đường thẳng
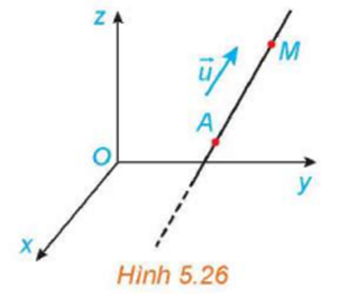
Trong không gian ![]() , một vật thể chuyển động với vectơ vận tốc không đổi
, một vật thể chuyển động với vectơ vận tốc không đổi ![]() và xuất phát từ điểm
và xuất phát từ điểm ![]() (H.5.26).
(H.5.26).
a) Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm mà nó đi qua và vectơ chỉ phương của đường thẳng đó)?
b) Giả sử tại thời điểm ![]() tính từ khi xuất phát, vật thể ở vị trí
tính từ khi xuất phát, vật thể ở vị trí ![]() Tính
Tính ![]() theo
theo ![]() và
và ![]() .
.
Giải nhanh:
a) Vật thể chuyển động trên đường thẳng qua A và song song với giá của vectơ ![]()
b) Tại thời điểm ![]() tính từ khi xuất phát, vật thể ở vị trí
tính từ khi xuất phát, vật thể ở vị trí ![]() nên:
nên: ![]()
![]()
![]()
![]()
Luyện tập 2. Trong không gian Oxyz, cho đường thẳng ![]() :
: ![]()
a) Hãy chỉ ra hai điểm thuộc ![]() và một vectơ chỉ phương của ∆.
và một vectơ chỉ phương của ∆.
b) Viết phương trình tham số của đường thẳng đi qua gốc toạ độ ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Giải nhanh:
a)![]() và
và ![]()
b) Đường thẳng ![]() :
: ![]()
c) Phương trình chính tắc của đường thẳng
Hoạt động 3. Hình thành khái niệm phương trình chính tắc của đường thẳng
Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() (a, b, c là các số khác 0).
(a, b, c là các số khác 0).
a) Điểm ![]() thuộc
thuộc ![]() khi và chỉ khi hai vectơ
khi và chỉ khi hai vectơ ![]() và
và ![]() có mối quan hệ gì?
có mối quan hệ gì?
b) Điểm ![]() thuộc
thuộc ![]() khi và chỉ khi các phân số
khi và chỉ khi các phân số ![]() có mối quan hệ gì?
có mối quan hệ gì?
Giải nhanh:
a) ![]() và
và ![]() cùng phương
cùng phương
b) ![]()
Luyện tập 3.
Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]() . Hãy chỉ ra một vecto chỉ phương của
. Hãy chỉ ra một vecto chỉ phương của ![]() và 2 điểm thuộc
và 2 điểm thuộc ![]()
Giải nhanh:
2 điểm ![]() và
và ![]() thuộc
thuộc ![]()
![]() là một vecto chỉ phương của
là một vecto chỉ phương của ![]()
Luyện tập 4.
Trong không gian ![]() , viết phương trình tham số và phương trình chính tắc của đường thẳng
, viết phương trình tham số và phương trình chính tắc của đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Giải nhanh:
Phương trình tham số của ![]()
![]()
Phương trình chính tắc của ![]()
![]()
Luyện tập 5.
Trong không gian ![]() , viết phương trình tham số của đường thẳng
, viết phương trình tham số của đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và vuông góc với mặt phẳng
và vuông góc với mặt phẳng ![]()
Giải nhanh:
![]()
d) Lập phương trình đường thẳng đi qua hai điểm
Hoạt động 4. Lập phương trình đường thẳng đi qua hai điểm
Trong không gian ![]() , cho hai điểm phân biệt
, cho hai điểm phân biệt ![]()
a) Hãy chỉ ra một vecto chỉ phương của đường thẳng ![]()
b) Viết phương trình đường thẳng ![]()
Giải nhanh:
a) ![]()
b)Phương trình tham số là:
![]()
Phương trình chính tắc là:
![]() với điều kiện
với điều kiện ![]()
Luyện tập 6.
Trong không gian ![]() , viết phương trình đường thẳng đi qua hai điểm
, viết phương trình đường thẳng đi qua hai điểm ![]()
Giải nhanh:
![]()
Vận dụng 1.
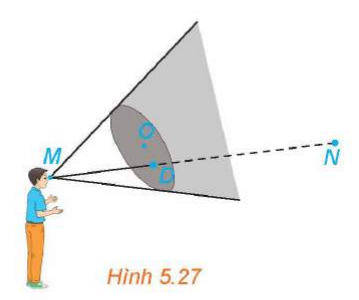
(H.5.27) Trong tình huống mở đầu hãy thực hiện các bước sau và trả lời câu hỏi đã được nêu ra.
Trong không gian ![]() , mắt một người quan sát đặt ở điểm
, mắt một người quan sát đặt ở điểm ![]() và vật cần quan sát đặt tại điểm
và vật cần quan sát đặt tại điểm ![]() ). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm
). Một tấm bìa chắn đường truyền của ánh sáng có dạng hình tròn với tâm ![]() , bán kính bằng 3 và đặt trong mặt phẳng
, bán kính bằng 3 và đặt trong mặt phẳng ![]() . Hỏi tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm
. Hỏi tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm ![]() hay không?
hay không?
a) Viết phương trình tham số của đường thẳng ![]() .
.
b) Tính toạ độ giao điểm ![]() của đường thẳng
của đường thẳng ![]() với mặt phẳng
với mặt phẳng ![]() .
.
c) Hỏi điểm ![]() có nằm giữa hai điểm
có nằm giữa hai điểm ![]() và
và ![]() hay không?
hay không?
Giải nhanh:
a)![]()
b) ![]()
c) Ta có: ![]()
![]()
![]()
![]()
Mặt khác ![]() thuộc đường thẳng
thuộc đường thẳng ![]() nên 3 điểm
nên 3 điểm ![]() thẳng hàng
thẳng hàng
![]() nằm giữa 2 điểm
nằm giữa 2 điểm ![]()
Như vậy tấm bìa có che khuất tầm nhìn của người quan sát đối với vật đặt ở điểm ![]()
2. HAI ĐƯỜNG THẲNG VUÔNG GÓC
Hoạt động 5. Tìm điều kiện để hai đường thẳng vuông góc
Trong không gian Oxyz, cho 2 đường thẳng ![]() tương ứng có vecto chỉ phương
tương ứng có vecto chỉ phương ![]() .
.
a) Hai đường thẳng ![]() và
và ![]() vuông góc với nhau khi và chỉ khi 2 giá của
vuông góc với nhau khi và chỉ khi 2 giá của ![]() có mối quan hệ gì?
có mối quan hệ gì?
b) Tìm điều kiện đối với ![]() để
để ![]() và
và ![]() vuông góc với nhau.
vuông góc với nhau.
Giải nhanh:
a) ![]() ⊥
⊥ ![]() <=> 2 giá của
<=> 2 giá của ![]() vuông góc với nhau
vuông góc với nhau
b) Nếu ![]() ⊥
⊥ ![]() thì 2 giá của
thì 2 giá của ![]() vuông góc với nhau. Khi đó
vuông góc với nhau. Khi đó ![]() .
.
Luyện tập 7.
Trong không gian ![]() , cho đường thẳng
, cho đường thẳng ![]()
![]() Hỏi đường thẳng
Hỏi đường thẳng ![]() có vuông góc với trục
có vuông góc với trục ![]() hay không?
hay không?
Giải nhanh:
Đường thẳng ![]() và trục Oz có vecto chỉ phương lần lượt là
và trục Oz có vecto chỉ phương lần lượt là ![]()
Do ![]() nên
nên ![]() không ⊥ trục
không ⊥ trục ![]()
Vận dụng 2.
Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian ![]() , hai con đường đó tương ứng thuộc hai đường thẳng:
, hai con đường đó tương ứng thuộc hai đường thẳng:
![]()
Hỏi hai con đường trên có vuông góc với nhau hay không?
Giải nhanh:
Các đường thẳng ![]() và
và ![]() có vecto chỉ phương lần lượt là:
có vecto chỉ phương lần lượt là:
![]()
Do ![]() )
)![]() nên
nên ![]() ⊥
⊥ ![]()
3. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
Hoạt động 6. Xác định vị trí tương đối giữa hai đường thẳng
Trong không gian Oxyz, cho hai đường thẳng ![]() và
và ![]() lần lượt đi qua các điểm
lần lượt đi qua các điểm ![]() và tương ứng có vecto chỉ phương phương
và tương ứng có vecto chỉ phương phương ![]() (H.5.29).
(H.5.29).
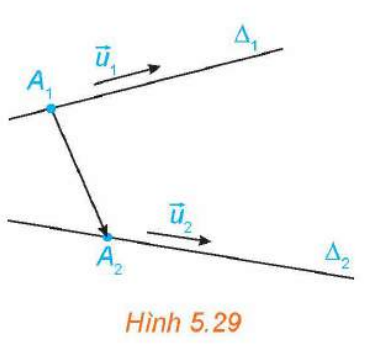
a) Tìm điều kiện đối với ![]() để
để ![]() và
và ![]() song song hoặc trùng nhau.
song song hoặc trùng nhau.
b) Giả sử ![]() và
và ![]() thì
thì ![]() và
và ![]() có cắt nhau hay không?
có cắt nhau hay không?
c) Giả sử ![]() thì
thì ![]() và
và ![]() có chéo nhau hay không?
có chéo nhau hay không?
Giải nhanh:
a) Để ![]() //
// ![]() hoặc trùng nhau thì giá của 2 vecto
hoặc trùng nhau thì giá của 2 vecto ![]() song song hoặc trùng nhau.
song song hoặc trùng nhau.
Do đó 2 vecto ![]() cùng phương với nhau
cùng phương với nhau
b) Vì ![]() và
và ![]()
![]() . Do đó,
. Do đó, ![]()
![]() và
và ![]() cắt nhau
cắt nhau
c) Vì ![]() và
và ![]() chéo nhau
chéo nhau
Luyện tập 8.
Trong không gian ![]() , chứng minh hai đường thẳng sau song song với nhau:
, chứng minh hai đường thẳng sau song song với nhau:
![]() và
và ![]()
Giải nhanh:
Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Do ![]() và
và ![]() không thuộc
không thuộc ![]() (
(![]() nên
nên ![]() //
// ![]()
Luyện tập 9.
Trong không gian ![]() , cho hai đường thẳng:
, cho hai đường thẳng: ![]() và
và ![]() Chứng minh rằng:
Chứng minh rằng:
a) Hai đường thẳng ![]() và
và ![]() song song với nhau;
song song với nhau;
b) Đường thẳng ![]() và trục
và trục ![]() chéo nhau;
chéo nhau;
c) Đường thẳng ![]() trùng với đường thẳng
trùng với đường thẳng ![]()
d) Đường thẳng ![]() cắt trục
cắt trục ![]() .
.
Giải nhanh:
Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
a) Do ![]() và
và ![]() không thuộc
không thuộc ![]() (
(![]() nên
nên ![]() //
// ![]()
b) Trục ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Ta có: ![]() và
và ![]()
Do ![]() nên đường thẳng
nên đường thẳng ![]() và trục
và trục ![]() chéo nhau
chéo nhau
c) Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Do ![]() và
và ![]() thuộc
thuộc ![]() (
(![]() nên hai đường thẳng
nên hai đường thẳng ![]() và
và ![]() trùng nhau
trùng nhau
d) Trục ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Ta có: ![]() và
và ![]()
Do ![]() và
và![]()
![]() nên đường thẳng
nên đường thẳng ![]() và trục
và trục ![]() cắt nhau
cắt nhau
Luyện tập 10.
Trong không gian Oxyz, xét vị trí tương đối giữa 2 đường thẳng:
![]()
![]()
Giải nhanh:
Các đường thẳng ![]() và
và ![]() có vecto chỉ phương là:
có vecto chỉ phương là:
![]()
![]() không cùng phương
không cùng phương
Xét hệ phương trình 2 ẩn t, s:
![]() (*)
(*)
Giải (1) và (2) ta được: ![]()
Thay vào (3): ![]() → Hệ phương trình (*) vô nghiệm
→ Hệ phương trình (*) vô nghiệm
Mà ![]() không cùng phương →
không cùng phương → ![]() và
và ![]() chéo nhau
chéo nhau
Vận dụng 3.
(H.5.30) Trong không gian ![]() , có hai vật thể lần lượt xuất phát từ
, có hai vật thể lần lượt xuất phát từ ![]() và
và ![]() với vận tốc không đổi tương ứng là
với vận tốc không đổi tương ứng là ![]() Hỏi trong quá trình chuyển động, hai vật thể có va chạm vào nhau hay không?
Hỏi trong quá trình chuyển động, hai vật thể có va chạm vào nhau hay không?
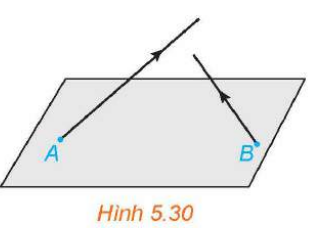
Giải nhanh:
Xét 2 đường thẳng ![]() và
và ![]() :
:
Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]()
Ta có: ![]() và
và
![]()
Do ![]() nên 2 đường thẳng
nên 2 đường thẳng ![]() và
và ![]() chéo nhau
chéo nhau
Như vậy trong quá trình chuyển động, hai vật thể không va chạm vào nhau
GIẢI BÀI TẬP
Bài 5.11 trang 48 sách toán 12 tập 2 kntt
Trong không gian ![]() , viết các phương trình tham số và chính tắc của đường thẳng
, viết các phương trình tham số và chính tắc của đường thẳng ![]() đi qua
đi qua ![]() và song song với đường thẳng
và song song với đường thẳng ![]() :
: ![]() .
.
Giải nhanh:
Phương trình tham số:
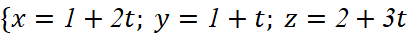
Phương trình chính tắc:
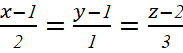
Bài 5.12 trang 48 sách toán 12 tập 2 kntt
Trong không gian ![]() , viết các phương trình tham số và chính tắc của đường thẳng
, viết các phương trình tham số và chính tắc của đường thẳng ![]() đi qua
đi qua ![]() và vuông góc với mặt phẳng
và vuông góc với mặt phẳng ![]()
Giải nhanh:
Phương trình tham số:
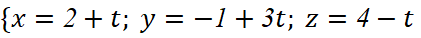
Phương trình chính tắc:
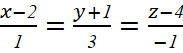
Bài 5.13 trang 48 sách toán 12 tập 2 kntt
Trong không gian ![]() , viết các phương trình tham số và chính tắc của đường thẳng
, viết các phương trình tham số và chính tắc của đường thẳng ![]() đi qua hai điểm
đi qua hai điểm ![]()
Giải nhanh:
Phương trình tham số là: ![]()
Phương trình chính tắc là: ![]()
Bài 5.14 trang 48 sách toán 12 tập 2 kntt
Trong không gian ![]() , cho hai đường thẳng:
, cho hai đường thẳng:
![]() và
và ![]() .
.
a) Chứng minh rằng ![]() và
và ![]() cắt nhau
cắt nhau
b) Viết phương trình mặt phẳng ![]() chứa
chứa ![]() và
và ![]()
Giải nhanh:
a) Phương trình tham số của đường thẳng ![]() là:
là: ![]()
Xét hệ phương trình 2 ẩn t, s:
![]() (*)
(*)
Giải (1) và (2), ta có: ![]()
Thay vào (3) ta có: ![]()
→ Hệ phương trình (*) có 1 nghiệm duy nhất
![]() và
và ![]() cắt nhau tại
cắt nhau tại ![]()
b) Các đường thẳng ![]() và
và ![]() có vecto chỉ phương lần lượt là:
có vecto chỉ phương lần lượt là:
![]()
Mặt phẳng ![]() chứa
chứa ![]() và
và ![]() nên
nên ![]() nhận vecto
nhận vecto ![]() làm vectơ pháp tuyến
làm vectơ pháp tuyến
Ta có: ![]()
Mặt phẳng ![]() chứa
chứa ![]() và
và ![]() nên có phương trình là:
nên có phương trình là:
![]()
![]()
Bài 5.15 trang 48 sách toán 12 tập 2 kntt
Trong không gian ![]() , cho hai đường thẳng:
, cho hai đường thẳng:
![]() và
và ![]()
a) Chứng minh rằng ![]() và
và ![]() song song với nhau
song song với nhau
b) Viết phương trình mặt phẳng ![]() chứa
chứa ![]() và
và ![]()
Giải nhanh:
a) Đường thẳng ![]() đi qua
đi qua ![]() và có
và có ![]()
Đường thẳng ![]() đi qua
đi qua ![]() và có
và có ![]()
Do ![]() và
và ![]() không thuộc
không thuộc ![]() (
(![]() nên
nên ![]() //
// ![]()
b) Mặt phẳng ![]() chứa
chứa ![]() và
và ![]() nên
nên ![]() nhận vecto
nhận vecto ![]() làm vectơ pháp tuyến
làm vectơ pháp tuyến
Ta có: ![]()
Mặt phẳng ![]() chứa điểm
chứa điểm ![]() và có
và có ![]() nên có phương trình là:
nên có phương trình là:
![]()
Bài 5.16 trang 48 sách toán 12 tập 2 kntt
Trong không gian Oxyz, xác định vị trí tương đối giữa 2 đường thẳng:
![]()
Giải nhanh:
Các đường thẳng ![]() và
và ![]() có vecto chỉ phương lần lượt là
có vecto chỉ phương lần lượt là ![]() không cùng phương
không cùng phương
Xét hệ phương trình 2 ẩn t, s:
![]() (*)
(*)
Giải (1) và (2) ta có: ![]()
Thay vào (3) ta có: ![]() → Hệ phương trình (*) vô nghiệm
→ Hệ phương trình (*) vô nghiệm
Mà ![]() không cùng phương →
không cùng phương → ![]() và
và ![]() chéo nhau
chéo nhau
Bài 5.17 trang 49 sách toán 12 tập 2 kntt
Tại một nút giao thông có hai con đường. Trên thiết kế, trong không gian ![]() , hai con đường đó thuộc hai đường thẳng lần lượt có phương trình:
, hai con đường đó thuộc hai đường thẳng lần lượt có phương trình:
![]() và
và ![]()
a) Hai con đường trên có vuông góc với nhau hay không?
b) Nút giao thông trên có phải là nút giao thông khác mức hay không?

Giải nhanh:
a) Đường thẳng ![]() đi qua
đi qua ![]() và có
và có ![]()
Đường thẳng ![]() đi qua
đi qua ![]() và có là
và có là ![]()
Do ![]() )
)![]() nên
nên ![]() ⊥
⊥ ![]()
Ta có: : ![]()
Do ![]() nên
nên ![]() và
và ![]() chéo nhau
chéo nhau
Như vậy nút giao thông trên là nút giao thông khác mức
Bài 5.18 trang 49 sách toán 12 tập 2 kntt
Trong không gian ![]() , một viên đạn được bắn ra từ điểm
, một viên đạn được bắn ra từ điểm ![]() và trong 3 giây, đầu đạn đi với vận tốc không đổi; vectơ vận tốc (trên giây) là
và trong 3 giây, đầu đạn đi với vận tốc không đổi; vectơ vận tốc (trên giây) là ![]() Hỏi viên đạn trên có bắn trúng mục tiêu trong mỗi tình huống sau hay không?
Hỏi viên đạn trên có bắn trúng mục tiêu trong mỗi tình huống sau hay không?
a) Mục tiêu đặt tại điểm ![]()
b) Mục tiêu đặt tại điểm ![]()
Giải nhanh:
a) Ta có: ![]()
Do ![]() nên hai vecto
nên hai vecto ![]() và
và ![]() không cùng phương.
không cùng phương.
Như vậy viên đạn trên không bắn trúng mục tiêu đặt tại điểm ![]()
b) Ta có: ![]()
Do ![]() , tức
, tức ![]()
=> ![]() và
và ![]() cùng phương và ngược hướng.
cùng phương và ngược hướng.
Như vậy viên đạn trên không bắn trúng mục tiêu đặt tại điểm ![]()
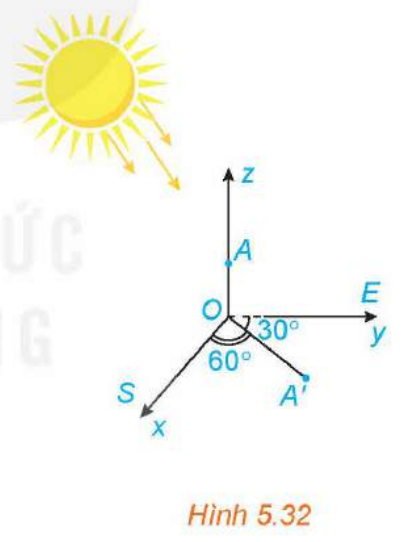
Bài 5.19 trang 49 sách toán 12 tập 2 kntt
Trên mặt đất phẳng, người ta dựng một cây cột thẳng cao 6m vuông góc với mặt đất, có chân cột đặt tại vị trí ![]() trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3 m về hướng
trên mặt đất. Tại một thời điểm, dưới ánh nắng mặt trời, bóng của đỉnh cột dưới mặt đất cách chân cột 3 m về hướng ![]() (hướng tạo với hướng nam góc
(hướng tạo với hướng nam góc ![]() và tạo với hướng đông góc
và tạo với hướng đông góc ![]() ) (H.5.32). Chọn hệ trục
) (H.5.32). Chọn hệ trục ![]() có gốc toạ độ là
có gốc toạ độ là ![]() , tia
, tia ![]() chỉ hướng nam, tia
chỉ hướng nam, tia ![]() chỉ hướng đông, tia
chỉ hướng đông, tia ![]() chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.
chứa cây cột, đơn vị đo là mét. Hãy viết phương trình đường thẳng chứa tia nắng mặt trời đi qua đỉnh cột tại thời điểm đang xét.
Giải nhanh:
![]() và
và ![]()
![]()
Đường thẳng ![]() đi qua
đi qua ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() nên có:
nên có:
Phương trình tham số:
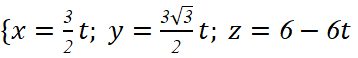
Phương trình chính tắc:
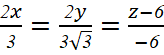
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận