Dễ hiểu giải Toán 12 Kết nối bài 3: Đường tiệm cận của đồ thị hàm số
Giải dễ hiểu bài 3: Đường tiệm cận của đồ thị hàm số. Trình bày rất dễ hiểu, nên tiếp thu Toán 12 Kết nối dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 3: ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
1. ĐƯỜNG TIỆM CẬN NGANG
Hoạt động 1: Nhận biết đường tiệm cận ngang.
Cho hàm số ![]() có đồ thị (C). Với
có đồ thị (C). Với ![]() , xét điểm
, xét điểm ![]() thuộc (C). Gọi
thuộc (C). Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên đường thẳng
trên đường thẳng ![]() (H.1.19).
(H.1.19).
- Tính khoảng cách
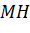 .
. - Có nhận xét gì về khoảng cách
 khi
khi 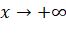 ?
?

Giải nhanh:
- Ta có các điểm
 và
và 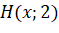 .
.

 (do
(do ![]() )
)
- Ta có:
 =>
=> 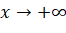 thì
thì 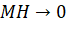 .
.
Luyện tập 1: Tìm tiệm cận ngang của đồ thị hàm số ![]() .
.
Giải nhanh:
Tiệm cận ngang của đồ thị hàm số ![]() là
là ![]() .
.
Vận dụng 1: Giải bài toán trong tình huống mở đầu.
Giải nhanh:
![]()
![]() khi
khi ![]() .
.
Trên Hình 1.18, khi ![]() thì
thì ![]() càng tiến sát tới trục hoành
càng tiến sát tới trục hoành ![]() nhưng không tiếp xúc.
nhưng không tiếp xúc.
2. ĐƯỜNG TIỆM CẬN ĐỨNG
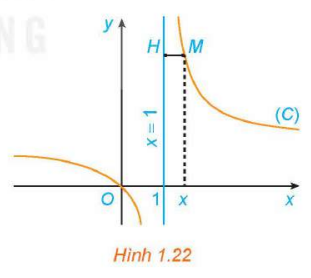
Hoạt động 2: Nhận biết đường tiệm cận đứng.
Cho hàm số ![]() có đồ thị (C). Với
có đồ thị (C). Với ![]() , xét điểm
, xét điểm ![]() thuộc (C). Gọi
thuộc (C). Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên đường thẳng
trên đường thẳng ![]() (H.1.22).
(H.1.22).
- Tính khoảng cách
 .
. - Khi
 thay đổi trên (C) sao cho khoảng cách
thay đổi trên (C) sao cho khoảng cách 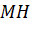 dần đến 0, có nhận xét gì về tung độ của điểm
dần đến 0, có nhận xét gì về tung độ của điểm  ?
?
Giải nhanh:
- Ta có các điểm
 và
và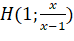
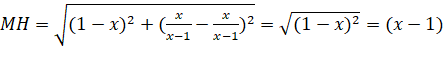 (do
(do ![]() )
)
- Khi
 thay đổi trên (C) sao cho khoảng cách
thay đổi trên (C) sao cho khoảng cách 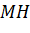 dần đến 0, ta thấy điểm
dần đến 0, ta thấy điểm  tiến đến
tiến đến  phía trên.
phía trên.
Luyện tập 2: Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ![]() .
.
Giải nhanh:
Ta có:  ;
;  . Vậy đồ thị hàm số có một tiệm cận ngang là
. Vậy đồ thị hàm số có một tiệm cận ngang là ![]() .
.
Ta có: ![]() ;
; ![]() . Vậy đồ thị hàm số có một tiệm cận đứng là
. Vậy đồ thị hàm số có một tiệm cận đứng là ![]() .
.
Vận dụng 2: Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là ![]() (triệu đồng), với
(triệu đồng), với ![]() .
.
Tìm tiệm cận đứng của đồ thị hàm số ![]() và nêu ý nghĩa thực tiễn của đường tiệm cận này.
và nêu ý nghĩa thực tiễn của đường tiệm cận này.
Giải nhanh:
![]() => Tiệm cận đứng là
=> Tiệm cận đứng là ![]() .
.
Tiệm cận đứng của đồ thị cho biết việc loại bỏ hoàn toàn loại tảo độc khỏi hồ nước đó là không thể dù có tốn bao nhiêu chi phí.
3. ĐƯỜNG TIỆM CẬN XIÊN
Hoạt động 3: Nhận biết đường tiệm cận xiên.
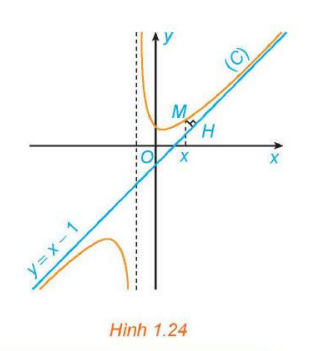
Cho hàm số ![]() có đồ thị (C) và đường thẳng
có đồ thị (C) và đường thẳng ![]() như Hình 1.24.
như Hình 1.24.
- Với
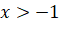 , xét điểm
, xét điểm  thuộc (C). Gọi
thuộc (C). Gọi  là hình chiếu vuông góc của M trên đường thẳng
là hình chiếu vuông góc của M trên đường thẳng  . Có nhận xét gì về khoảng cách
. Có nhận xét gì về khoảng cách 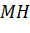 khi
khi  ?
? - Chứng tỏ rằng
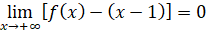 . Tính chất này thể hiện trên Hình 1.24 như thế nào?
. Tính chất này thể hiện trên Hình 1.24 như thế nào?
Giải nhanh:
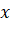 tiến dần đến
tiến dần đến  thì khoảng cách
thì khoảng cách  tiến dần đến 0.
tiến dần đến 0.- Ta có:
![]() .
.
=> Khoảng cách từ điểm ![]() trên (C) đến đường thẳng
trên (C) đến đường thẳng ![]() tiến đến 0 khi
tiến đến 0 khi ![]() .
.
Luyện tập 3: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số ![]() .
.
Giải nhanh:
![]() ;
;![]()
=> đồ thị có một tiệm cận đứng là đường thẳng ![]() .
.
![]()
![]() ;
;
![]()
=> đồ thị có một tiệm cận xiên là đường thẳng ![]() .
.
GIẢI BÀI TẬP
Bài 1.16 trang 25 sách toán 12 tập 1 kntt
Hình 1.26 là đồ thị của hàm số ![]() .
.
Sử dụng đồ thị này, hãy:
- Viết kết quả của các giới hạn sau:
 ;
; ;
;  ;
;  .
. - Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Giải nhanh:
 ;
; 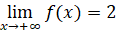 ;
;  ;
;  .
.- Hàm số có hai tiệm cận đứng là
 và
và  và một tiệm cận ngang là
và một tiệm cận ngang là  .
.
Bài 1.17 trang 25 sách toán 12 tập 1 kntt
Đường thẳng ![]() có phải là tiệm cận đứng của hàm số
có phải là tiệm cận đứng của hàm số ![]() không?
không?
Giải nhanh:
![]() ;
;
![]() ;
;![]()
=> ![]() không phải là tiệm cận đứng của hàm số.
không phải là tiệm cận đứng của hàm số.
Bài 1.18 trang 25 sách toán 12 tập 1 kntt
Tìm các tiệm cận của đồ thị các hàm số sau:
 ;
; .
.
Giải nhanh:
a)
![]() ;
;![]()
=> Hàm số có một tiệm cận ngang là ![]() .
.
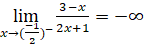 ;
;
=> Hàm số có tiệm cận đứng là ![]() .
.
b)
![]() ;
; ![]()
=> Hàm số không có tiệm cận đứng.
![]() ;
;![]()
=> Hàm số có một tiệm cận ngang là ![]() .
.
![]()
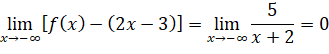

=> Hàm số có một tiệm cận xiên là đường thẳng ![]() .
.
Bài 1.19 trang 25 sách toán 12 tập 1 kntt
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất ![]() (sản phẩm) là
(sản phẩm) là
![]() (triệu đồng).
(triệu đồng).
Khi đó ![]() là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số
là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số ![]() giảm và
giảm và ![]() . Tính chất này nói lên điều gì?
. Tính chất này nói lên điều gì?
Giải nhanh:

Vì ![]() với mọi số thực
với mọi số thực ![]() nên hàm số
nên hàm số ![]() giảm.
giảm.
![]() (điều phải chứng minh)
(điều phải chứng minh)
=> Sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình giảm nhưng không dưới 2 triệu đồng.
Bài 1.20 trang 25 sách toán 12 tập 1 kntt
Một mảnh vườn hình chữ nhật có diện tích bằng 144 m2. Biết độ dài một cạnh của mảnh vườn là ![]() (m).
(m).
- Viết biểu thức tính chu vi
 (mét) của mảnh vườn.
(mét) của mảnh vườn. - Tìm các tiệm cận của đồ thị hàm số
 .
.
Giải nhanh:
- Độ dài cạnh còn lại của mảnh vườn là:
 (m)
(m)
=> Chu vi mảnh vườn ![]() (m)
(m)
- Ta có:
 ;
;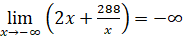
=> Đồ thị hàm số ![]() không có tiệm cận ngang.
không có tiệm cận ngang.
Ta có: ![]() ;
;![]()
=> Đồ thị hàm số ![]() có một tiệm cận đứng là
có một tiệm cận đứng là ![]() .
.
Ta có:![]()
=> Đồ thị hàm số ![]() có một tiệm cận xiên là
có một tiệm cận xiên là ![]() .
.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận