Lời giải Bài 4 Đề thi thử trường THPT chuyên Amtesdam Hà Nội

Lời giải bài 4:

Đề ra : 

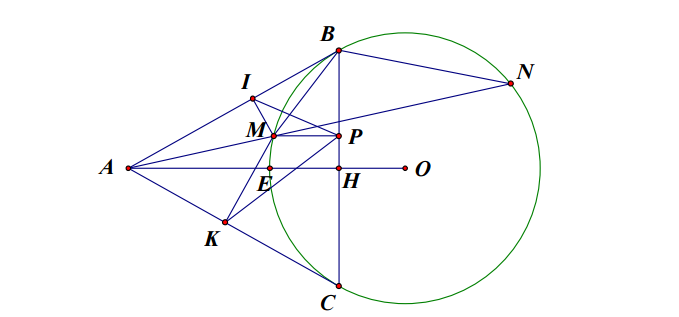
Từ một điểm A nằm ngoài đường tròn (O;R) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm) và một cát tuyến AMN ( M nằm giữa A và N). Gọi I, K, P lần lượt là hình chiếu vuông góc của M xuống các cạnh AB, AC, BC. Gọi E là điểm chính giữa cung nhỏ BC.

a) Chứng minh: AIMK là tứ giác nội tiếp đường tròn.

b) Gọi H là trung điểm đoạn BC. Chứng minh: AM.AN = AH. AO.

c) Chứng minh E là tâm đường tròn nội tiếp tam giác ABC.

Lời giải chi tiết :

a.   Ta có : $\widehat{AIM}=\widehat{AKM}=90^{\circ}$

=>   $\widehat{AIM}+\widehat{AKM}=180^{\circ}$

=>  Tứ giác AIMK là tứ giác nội tiếp đường tròn .    ( đpcm ) 

b.  Xét $\triangle ABM \sim \triangle ANB$  ( g-g )

=>  $AM.AN=AB^{2}$                   (*)

Xét  $\triangle ABO$ vuông tại B có BH là đường cao .

=>  $AH.AO=AB^{2}$                   (**)

Từ (*),(**)   =>  AM.AN = AH. AO.   ( đpcm )

c.  Vì  E là điểm chính giữa cung nhỏ BC   ( gt )

=>  $E\in AO$

=>   AE là phân giác trong của góc BAC .           (1)

Ta có :   $\widehat{ABE}=\widehat{BCE}=\widehat{CBE}$

=>   BE  là phân giác trong của góc ABC .           (2)

Từ (1) , (2)  =>  E là tâm đường tròn nội tiếp tam giác ABC.    ( đpcm )