Giải câu 6 trang 122 sách phát triển năng lực toán 9 tập 1

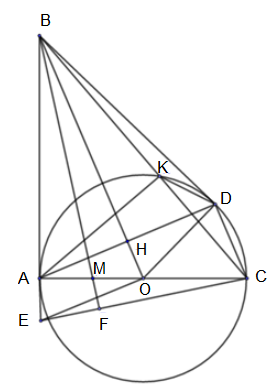
a, Ta có tam giác AKC thuộc đường tròn (O) có đường kính AC

=> Tam giác AKC vuông tại K

=> $\widehat{BKA}=90^{0}$

=> B, K, A cùng thuộc đường tròn đường kính BA (1)

Lại có BO $\perp $ AD tại H => $\widehat{BHA}=90^{0}$

=> B, H, A cùng thuộc đường tròn đường kính BA (2)

Từ (1) và (2) suy ra B, H, A, K cùng thuộc đường tròn đường kính BA (đpcm)

b, Xét tam giác OAD cân tại O (do OA = OD = R) có OB vuông góc với AD

=> OB là đường trung trực của cạnh AD (tính chất tam giác cân)

=> AB = BD (tính chất đường trung trực)

+ Xét tam giác ABO và DBO có:

• AB = BD
• AO = OD (= bán kính của đường tròn)
• BO chung

=> $\Delta $ABO = $\Delta $DBO (c - c -c )

=> $\widehat{BDO}=\widehat{BAO}=90^{0}$

=> BD $\perp $ OD

Suy ra BD là tiếp tuyến của đường tròn (O) (đpcm).

c, Xét tam giác vuông BOD có HD là đường cao

=> BH.BO = BD$^{2}$ (hệ thức lượng trong tam giác vuông) (3)

+ Xét tam giác BDK và tam giác BCD có:

• Góc CBD chung
• $\widehat{BDK}=\widehat{BCD}$ (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung chắn cung DK)

=> $\Delta $ABO $\sim $ $\Delta $DBO (g-g)

=> $\frac{BD}{BC}=\frac{BK}{BD}$ => BK.BC = BD$^{2}$ (4)

Từ (3) và (4) suy ra: BH.BO = BK.BC (đpcm)

d, Xét tam giác BEF và tam giác CEA có:

• $\widehat{ABM}=\widehat{ACE}$  (cùng phụ với góc BEC)
• $\widehat{CAE}=\widehat{BAM}=90^{0}$

=> $\Delta $BEF $\sim $ $\Delta $CEA (g-g)

=> $\frac{AM}{AE}=\frac{AB}{AC}$ => AB.AE =AM.AC (*)

Xét tam giác BOE vuông tại O có AO là đường cao:

=> AB.AE = AO$^{2}$ (**)

Từ (*) và (**) => AO$^{2}$ = AM.AC <=> AO$^{2}$ = 2AO.AM <=> 2AM = AO

Mà có AM + MO = AO => MO = AO - AM = 2AM - AM = AM

Vậy AM = MO (đpcm)