1. Một khu cắm trại tính chi phí cho mỗi nhóm cắm trại là 200000 đồng, cộng với 40000 đồng cho mỗi người, mỗi đêm.

a, Viết hàm số biểu thị lệ phí một đêm cho x người trong một trại.

b, Vẽ đồ thị hàm số trong câu a

c, Tính lệ phí một đêm của một trại có 6 người tham gia.

Hướng dẫn:

a, Hàm số biểu thị lệ phí một đêm cho x người trong một trại: 

                   y =  40000x + 200000 (đồng)

b, Vẽ đồ thị hàm số

c, Lệ phí một đêm của một trại có 6 người là:

y = 40000.6 + 200000 = 440000 (đồng)

2. Cho ba đường thẳng (d₁): y = -x + 1; (d₂): y = x + 1 và (d₃): y = -1

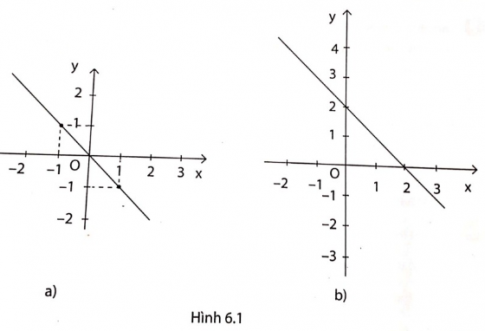
a, Vẽ ba đường thẳng đã cho trên cùng một mặt phẳng tọa độ Oxy.

b, Xác định góc tạo bởi mỗi đường thẳng (d₁), (d₂) với trục Ox.

c, Gọi giao điểm của hai đường thẳng (d₁), (d₂) là A, giao điểm của đường thẳng (d₃) với hai đường thẳng (d₁), (d₂) theo thứ tự B và C. Tìm tọa độ các điểm A, B, C.

d, Bạn Minh nói rằng tam giác ABC là tam giác vuông cân. Minh nói đúng hay sai? Giải thích. Tính diện tích tam giác ABC.

Hướng dẫn:

a, Vẽ đồ thị hàm số:

b, Gọi góc tạo bởi (d₁), (d₂) với trục Ox lần lượt là $\beta $ và $\alpha $.

Ta có: tan$\alpha $ = 1 => $\alpha $ = 45$^{0}$

$\beta $ = 180$^{0}$ - 45$^{0}$ = 135$^{0}$

c, Gọi tọa độ điểm A, B, C lần lượt là: A(x₀; y₀); B(x₁; y₁); C(x₂; y₂)

• A là giao điểm của (d₁) và (d₂) => x₀ + 1 = -x₀ + 1 => x₀ = 0 => y₀ = 1

=> Tọa độ điểm A là A(0; 1)

• B là giao điểm của (d₁) và (d₃) => $\left\{\begin{matrix}y_{1}=-1 &  & \\ y_{1}=-x_{1}+1 &  & \end{matrix}\right.$ => -1 = -x₁ + 1 => x₁ = 2

=> Tọa độ điểm B là: B(2; -1)

• C là giao điểm của (d₂) và (d₃) => $\left\{\begin{matrix}y_{2}=-1 &  & \\ y_{2}=x_{2}+1 &  & \end{matrix}\right.$ => -1 = x₂ + 1 => x₂ = -2

=> Tọa độ điểm C là: C(-2; -1)

d, Ta có AB = AC = $\sqrt{2^{2}+2^{2}}=2\sqrt{2}$; BC = 2 + 2 = 4

$BC^{2}=4^{2}=16$; $AB^{2}+AC^{2}=(2\sqrt{2})^{2}+(2\sqrt{2})^{2}=16$ => $BC^{2}=AB^{2}+AC^{2}$

=> Tam giác ABC vuông cân tại A

=> Bạn Minh nói đúng.

S_ABC = $\frac{1}{2}$.AC.AB = $\frac{1}{2}.2\sqrt{2}.2\sqrt{2}$ = 4