Giải phát triển năng lực toán 9 bài 2: Tỉ số lượng giác của góc nhọn
Giải bài 2: Tỉ số lượng giác của góc nhọn - Sách phát triển năng lực trong môn toán 9 tập 1 trang 67. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
1. Khái niệm tỉ số lượng giác của một góc nhọn
a, Em hãy cùng bạn thảo luận để hoàn thaành bảng sau:
Hướng dẫn:
| Cho | So sánh và giải thích | |
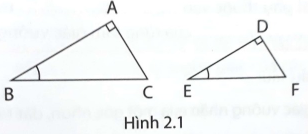
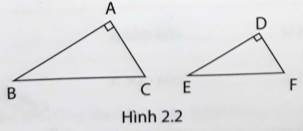
| Nội dung 1 | $\widehat{A}=\widehat{D}=90^{0},\widehat{B}=\widehat{E}$ | $\frac{AC}{AB}$ và $\frac{DF}{DE}$ $\frac{AC}{AB}=\frac{DF}{DE}$ Vì $\Delta ACB\sim \Delta DFE$ (g-g) |
| Nội dung 2 | $\widehat{A}=\widehat{D}=90^{0}$; $\frac{AC}{AB}=\frac{DF}{DE}$ | $\widehat{B}$ và $\widehat{E}$ $\widehat{B}=\widehat{E}$ Vì Vì $\Delta ACB\sim \Delta DFE$ (c-g-c) |
b, Cho góc nhọn $\widehat{xOy}=\alpha $, trên tia Ox lấy điểm M bất kì, qua M kẻ đường thẳng vuông góc với Oy, cắt Oy tại N. Em hãy tính tỉ số $\frac{MN}{ON}$ trong mỗi trường hợp sau đây:
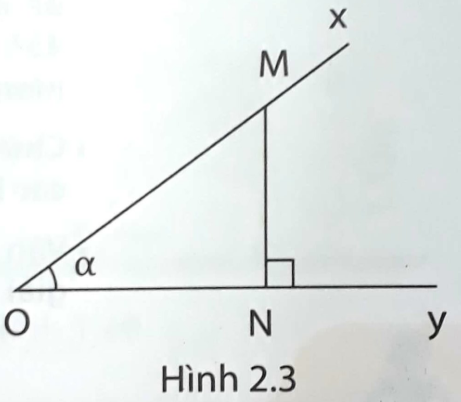
i. $\alpha =45^{0}$ ii. $\alpha =60^{0}$
Hướng dẫn:
i, $\alpha =45^{0}$ => $\widehat{NMO}=90{0}-45^{0}=45^{0}$ => Tam giác MNO vuông cân tại O
=> $\frac{MN}{ON}=1$
ii. $\alpha =60^{0}$ => $\frac{MN}{ON}=1,73$
Nhận xét:
Trong các tam giác vuông có một góc nhọn bằng $\alpha $, tỉ số giữa cạnh đối và cạnh kề của góc nhọn $\alpha $ chỉ phụ thuộc vào độ lớn của $\alpha $ mà không phụ thuộc vào độ dài các cạnh của từng tam giác vuông.
c, Em hãy thực hiện các yêu cầu sau:
- Vẽ một góc nhọn $\alpha $, vẽ tam giác vuông nhận $\alpha $ là một góc nhọn, đặt tên tam giác.
- Chỉ ra các cạnh đối, cạnh kề của góc $\alpha $, cạnh huyền của tam giác.
- Đọc SGK Toán 9 - tập 1, trang 72, diền vào chỗ chấm để hoàn thành bảng định nghĩa các tỉ số lượng giác của góc nhọn $\alpha $.
Hướng dẫn:
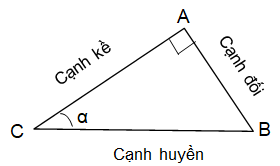
Kí hiệu: cạnh đối = đ; Cạnh kề = k; cạnh huyền = h
Ta có:
- $sin\alpha =\frac{đ}{h}$ được gọi là sin của góc $\alpha $
- $cos\alpha =\frac{k}{h}$ được gọi là cosin của góc $\alpha $
- $tan\alpha =\frac{đ}{k}$ được gọi là tang của góc $\alpha $
- $cot\alpha =\frac{k}{đ}$ được gọi là cotang của góc $\alpha $
d, Từ kết quả của hoạt dộng 1b và 1c, tính tỉ số lượng giác của góc $45^{0}$ và $60^{0}$
Hướng dẫn:
$sin45^{0}$ = 0,707 $sin60^{0}$ = 0,866
$cos45^{0}$ = 0,707 $cos60^{0}$ = 0,5
$tan45^{0}$ = 1 $tan60^{0}$ = 1,732
$cot45^{0}$ = 1 $cot60^{0}$ = 0,577
2. a, Từ hoạt động 1c điền dấu (>, <, =) thích hợp vào ô trống để được khẳng định đúng với mọi góc nhọn $\alpha $ và giải thích.
Hướng dẫn:
$sin\alpha $ > 0 $cos\alpha $ > 0
$sin\alpha $ < 1 $cos\alpha $ < 1
$tạn\alpha $ = $\frac{sin\alpha }{cos\alpha }$
$\frac{cos\alpha }{sin\alpha }$ = $cot\alpha $
$sin^{2}\alpha +cos^{2}\alpha $ = 1
b, Trong hình vẽ tam giác vuông của hoạt động 1c, gọi $\beta $ là góc nhọn còn lại
- Em hãy lập các tỉ số lượng giác của góc $\beta $.
- Tìm các cặp tỉ số lượng giác bằng nhau của góc $\alpha $ và $\beta $.
- Từ kết quả thu được, em hãy điền các tỉ số lượng giác thích hợp vào chỗ chấm để hoàn thành liên hệ giữa tỉ số lượng giác của hai góc phụ nhau.
Hướng dẫn:
+ Tỉ số lượng giác của góc $\beta $
- $sin\beta =\frac{AC}{BC}$ $cos\beta =\frac{AB}{BC}$
- $tan\beta =\frac{AC}{AB}$ $cot\beta =\frac{AB}{AC}$
+ Các cặp tỉ số lượng giác bằng nhau
- $sin\alpha =cos\beta $ $cos\alpha =sin\beta $
- $tan\alpha =cot\beta $ $cot\alpha =tan\beta $
+ Hoàn thành bảng:
- $sin\alpha =cos(90^{0}-\alpha )$ $cos\alpha =sin(90^{0}-\alpha )$
- $tan\alpha =cot(90^{0}-\alpha )$ $cot\alpha =tan(90^{0}-\alpha )$
c, Từ kết quả của hoạt động 1d và 2b em hãy tìm các tỉ số lượng giác của góc $30^{0}$, từ đó hoàn thành bảng lượng giác của các góc đặc biệt.
Hướng dẫn:
$\alpha $ Tỉ số lượng giác | $30^{0}$ | $45^{0}$ | $60^{0}$ |
| sin $\alpha $ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ |
| cos $\alpha $ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ |
| tan $\alpha $ | $\frac{\sqrt{3}}{3}$ | 1 | $\sqrt{3}$ |
| cot $\alpha $ | $\sqrt{3}$ | 1 | $\frac{\sqrt{3}}{3}$ |
d, Quan sát bảng thu được sau hoạt động 2c, em có nhận xét gì vè sự tăng, giảm của các tỉ số lượng giác sin $\alpha $, cos $\alpha $, tan $\alpha $, cot $\alpha $ khi góc $\alpha $ tăng?
Nhận xét bảng 2c cũng đúng trong trường hợp $\alpha $ là góc nhọn bất kì. Em hãy điền từ thích hợp vào chỗ chấm để hoàn thành nhận xét
Hướng dẫn:
- Khi góc $\alpha $ tăng thì sin $\alpha $ tăng, cos $\alpha $ giảm, tan $\alpha $ tăng, cot $\alpha $ giảm.
- Khi góc $\alpha $ tăng từ $0^{0}$ đến $90^{0}$ thì:
- sin $\alpha $ và an $\alpha $ tăng.
- cos $\alpha $ và cot $\alpha $ giảm.
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9


Bình luận