Giải câu 3 trang 124 sách toán VNEN lớp 7 tập 1

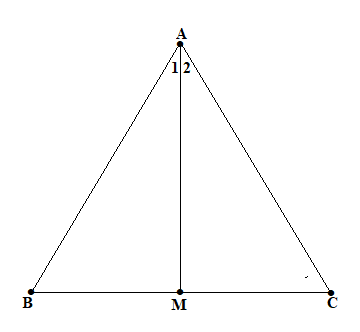
a) Xét $\bigtriangleup ABM$ và $\bigtriangleup ACM$

AB = AC (theo giả thiết);

$\widehat{A_{1}} = \widehat{A_{2}} $ (theo giả thiết AM là tia phân giác góc A);

AM chung;

Do đó $\bigtriangleup ABM = \bigtriangleup ACM$ (c.g.c)

$\Rightarrow $ MB = MC (hai cạnh tương ứng)

Xét đoạn thẳng BC có MB = MC (cmt) và M nằm giữa B và C, suy ra M là trung điểm của BC.

b) Theo câu a) $\bigtriangleup ABM = \bigtriangleup ACM$ $\Rightarrow $ $\widehat{AMB} = \widehat{AMC}$.

Mà hai góc AMB và AMC là hai góc kề bù nên: $\widehat{AMB} + \widehat{AMC} = 180^{\circ}$.

Suy ra: $\widehat{AMB} = \widehat{AMC} = 180 : 2 = 90^{\circ}$.

Hay AM $\perp $ BC (đpcm)