Giải câu 2 trang 123 sách toán VNEN 7 tập 1
Câu 2: Trang 123 sách toán VNEN lớp 7 tập 1
a) Vẽ tam giác ABC, biết $\widehat{A} = 90^{\circ}$, AB = AC = 3 cm. Sau đó đo góc B và góc C.
b) Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây (h.82) bằng nhau theo trường hợp cạnh – góc – cạnh:
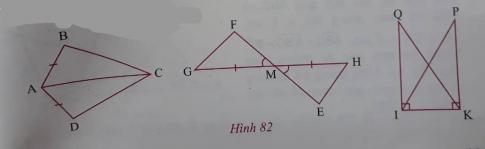
*) $\bigtriangleup ABC = \bigtriangleup ADC$;
**) $\bigtriangleup FMG = \bigtriangleup EMH$;
***) $\bigtriangleup QIK = \bigtriangleup PKI$.
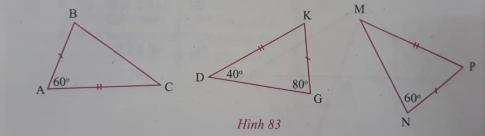
c) Trên hình 83 hai tam giác nào bằng nhau? Vì sao?
a) Các em thực hiện các bước vẽ tam giác sử dụng thước thẳng và compa để được hình vẽ như dưới đây:
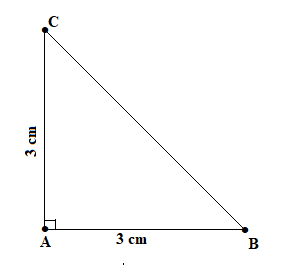
Dùng thước đo góc để đo góc B và góc C, ta được: $\widehat{B} = \widehat{C} = 45^{\circ}$.
b) *) $\bigtriangleup ABC$ và $\bigtriangleup ADC$ có: AC chung; AB = AD.
$\Rightarrow $ Điều kiện để $\bigtriangleup ABC = \bigtriangleup ADC$ theo trường hợp cạnh – góc – cạnh là: $\widehat{BAC} = \widehat{CAD}$.
**) $\bigtriangleup FMG$ và $\bigtriangleup EMH$ có: GM = MH; $\widehat{FMG} = \widehat{HME}$.
$\Rightarrow $ Điều kiện để $\bigtriangleup FMG = \bigtriangleup EMH$ theo trường hợp cạnh – góc – cạnh là: FM = ME.
***) $\bigtriangleup QIK$ và $\bigtriangleup PKI$ có: IK chung; $\widehat{QIK} = \widehat{PKI} = 90^{\circ}$.
$\Rightarrow $ Điều kiện để $\bigtriangleup QIK = \bigtriangleup PKI$ theo trường hợp cạnh – góc – cạnh là: QI = PK.
c) Xét tam giác KGD có: $\widehat{DKG} = 180^{\circ} - \widehat{KGD} - \widehat{KDG} = 180^{\circ} - 80^{\circ} - 40^{\circ} = 60^{\circ}$.
Từ hình vẽ ta thấy $\bigtriangleup ABC = \bigtriangleup KGD$ vì: AB = KG; AC = KD; $\widehat{A} = \widehat{K} = 60^{\circ}$.

Bình luận