Giải bài tập 73 trang 85 SBT toán 8 tập 2 cánh diều:
Bài tập 73 trang 85 SBT toán 8 tập 2 cánh diều:
Cho tam giác ABC vuông tại A, có đường phân giác AD. Vẽ hình vuông MNPQ ở đó M thuộc cạnh AB, N thuộc cạnh AC, P và Q thuộc cạnh BC. Gọi E và F lần lượt là giao điểm của BN và MQ; CM và NP (Hình 60).
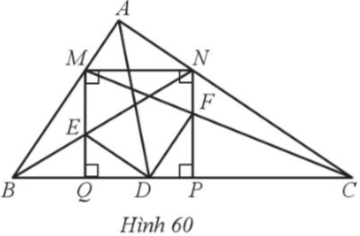
Chứng minh:
a) DE song song với AC;
b) DE = DF.
a) Ta có $\frac{BE}{EN}=\frac{BQ}{QP}=\frac{BQ}{MQ}=\frac{AB}{AC}=\frac{BD}{DC}$
=> DE // NC hay DE // AC.
b) Do DE // AC nên $\frac{DE}{CN}=\frac{BD}{BC}$ hay DE = $\frac{BD}{BC}.CN$.
Tương tự: DF = $\frac{CD}{BC}.BM$. => $\frac{DE}{DF}=\frac{BD}{CD}.\frac{CN}{BM}$.
Mặt khác, $\frac{BD}{CD}=\frac{AB}{AC}$ và $\frac{CN}{BM}=\frac{AC}{AB}$ nên $\frac{DE}{DF}$ = 1 hay DE = DF.
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận