Giải bài tập 66 trang 84 SBT toán 8 tập 2 cánh diều:
Bài tập 66 trang 84 SBT toán 8 tập 2 cánh diều:
Cho điểm M thuộc đoạn thẳng AB, với MA = a, MB = b. Vẽ hai tam giác đều AMC và BMD; gọi E là giao điểm của AD và CM, F là giao điểm của DM và BC (Hình 58).
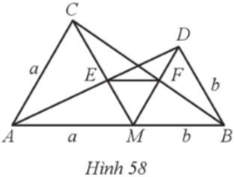
a) Chứng minh EF // AB.
b) Tính ME, MF theo a, b.
a) Ta có $\widehat{DMB}=\widehat{CAM}$ = 60°, $\widehat{DBM}=\widehat{CMA}$ = 60°. Suy ra MD // AC, DB // CM.
Do MD // AC nên $\frac{EC}{EM}=\frac{AC}{DM}=\frac{a}{b}$ (theo định lí Thalès).
Tương tự, do DB // CM nên $\frac{CF}{FB}=\frac{CM}{DB}=\frac{a}{b}$.
Từ đó, ta có: $\frac{EC}{EM}=\frac{CF}{FB}=\frac{a}{b}$ nên EF // MB hay EF // AB.
b) Từ EF // AB suy ra tam giác EMF là tam giác đều.
Từ đó, ta có: $\frac{EC}{CM}=\frac{EF}{MB}=\frac{EC+EF}{CM+MB}=\frac{a}{a+b}$.
=> EF = $\frac{ab}{a+b}$.
Vì tam giác MEF là tam giác đều nên ME = MF = EF = $\frac{ab}{a+b}$.

Bình luận