Giải bài tập 68 trang 85 SBT toán 8 tập 2 cánh diều:
Bài tập 68 trang 85 SBT toán 8 tập 2 cánh diều:
Cho tam giác ABC có ba góc nhọn, điểm I thuộc cạnh BC và IM, IN lần lượt là đường phân giác của các góc AIC và AB. Chứng minh: AN. BI. CM = BN. IC. AM.
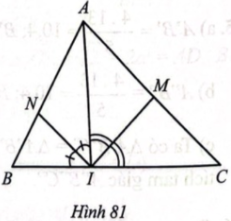
Áp dụng tính chất đường phân giác vào các tam giác ABI, AIC, ta có:
$\frac{AN}{NB}=\frac{AI}{BI}$; $\frac{CM}{MA}=\frac{IC}{AI}$.
=>$\frac{BI}{IC}.\frac{AN}{NB}.\frac{CM}{MA}=\frac{BI}{IC}.\frac{AI}{BI}.\frac{IC}{AI}$ = 1.
Do đó: AN. BI. CM = BN. IC. AM.
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận