Giải bài tập 67 trang 85 SBT toán 8 tập 2 cánh diều:

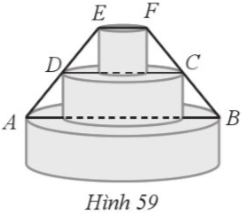
Tầng giữa có đường kính CD là: 32 - 12 = 20 cm.

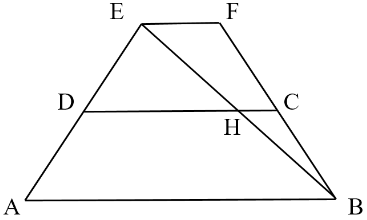
Ta có: EF // AB; D, C lần lượt là trung điểm của EA và FB => DC // EF // AB.

Xét tam giác EDH và EAB có DH // AB => ΔEDH ᔕ ΔEAB.

=> $\frac{DE}{AE}=\frac{DH}{AB}=\frac{1}{2}$.

=> DH = $\frac{AB.DE}{AE}=\frac{32.1}{2}$ = 16 cm.

Độ dài HC = DC - DH = 20 - 16 = 4 cm.

Xét tam giác BHC và BEF có HC // EF => ΔBHC ᔕ ΔBEF.

=> $\frac{HC}{EF}=\frac{BC}{BF}=\frac{1}{2}$

=> EF = 2.HC = 2.4 = 8 cm.

Vậy độ dài đường kính tầng trên cùng EF = 8 cm.