Giải Bài tập 2.32 trang 57 sgk Toán 11 tập 1 Kết nối

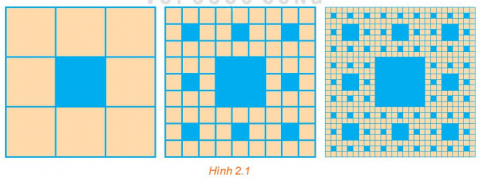
+ Chia lần 1: Hình vuông màu vàng lớn có cạnh bằng 1 đơn vị thì có diện tích bằng 1 (đvdt). Chia hình vuông này thành 9 hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh, thì hình vuông màu xanh đầu tiên này có diện tích bằng $\frac{1}{9}$ (đvdt).

+ Chia lần 2: 8 hình vuông màu vàng còn lại, mỗi hình vuông này lại được chia thành 9 hình vuông con và tiếp tục tô xanh hình vuông chính giữa, khi đó mỗi hình vuông xanh nhỏ hơn có diện tích $S_{1}=\frac{1}{9}.\frac{1}{9}=\frac{1}{9^{2}}$, 8 hình vuông xanh nhỏ hơn có diện tích bằng $8S_{1}$.

Cứ tiếp tục như vậy, mỗi lần chia ta sẽ tạo thành 8 hình vuông xanh nhỏ hơn tiếp đối với mỗi ô vuông vàng nhỏ.

Do đó, quá trình này được tiếp tục lặp lại năm lần, thì trừ lần đầu tiên, 4 lần sau, mỗi lần chia diện tích ô vuông xanh tạo thành lập thành một cấp số nhân có $u_{1}=8.\frac{1}{9^{2}}$ và công bội $q=8.\frac{1}{9}$

Vậy tổng diện tích các hình vuông được tô màu xanh là

$S=\frac{1}{9}+\frac{8.\frac{1}{9^{2}}(1-(\frac{8}{9})^{4})}{1-\frac{8}{9}}=\frac{26281}{59049}$ (đvdt)