Đề số 4: Đề kiểm tra toán 8 Kết nối bài 14 Hình thoi và hình vuông

Câu 1: 

Xét tứ giác MNPQ có: MP và NQ cắt nhau tại trung điểm của mỗi đường , suy ra MNPQ là hình bình hành. 

Ta lại có MP vông góc với NQ nên MNPQ là hình thoi 

=> AB = BC = CD = AD (1)

Mặt khác, NO là đường trung tuyến ứng với cạnh MP, $MO = \frac{1}{2} MP$ nên tam giác MNP vuông tại N hay $\widehat{MNP}=90^{\circ}$

Tương tự ta có: $\widehat{NPQ}=\widehat{MQP}=\widehat{NMQ}=\widehat{MNP}=90^{\circ}$ (2)

Từ (1)(2) suy ra MNPQ là hình vuông

Xét tứ giác URST có: UR = RS = ST = UT, $\widehat{URS}=90^{\circ}$

=> URST là hình vuông

Câu 2

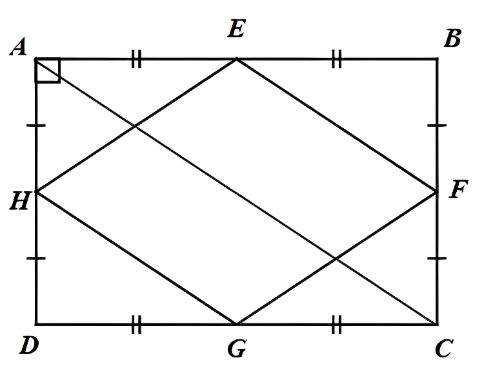
E, F lần lượt là trung điểm của AB và BC

⇒ EF là đường trung bình của tam giác ABC

⇒ EF//AC và $EF=\frac{1}{2}AC$ (1)

H, G lần lượt là trung điểm của AD và DC

⇒ HG là đường trung bình của tam giác ACD

⇒ HG // AC và $HG=\frac{1}{2}AC$ (2)

Từ (1) và (2) ⇒ EF//HG và EF = HG

Vậy tứ giác EFGH là hình bình hành.

Tứ giác ABCD có AB=CD và AD=BC ⇒ Tứ giác ABCD là hình bình hành.

Mà $\widehat{BAD}=90^{\circ}$ ⇒ ABCD là hình chữ nhật.

Xét ΔEBFvà ΔCGFcó :

EB = EC (gt)

BF = FC(gt)

$\widehat{EBF}=\widehat{GCF}$

⇒ ΔEBF = ΔGCF(c.g.c) ⇒ EF = GF

Chứng minh tương tự ta có GF = GH, GH = EF ⇒ EF = GF = GH = EH

Do đó tứ giác EFGH là hình thoi.