Đề số 2: Đề kiểm tra toán 8 Kết nối bài 2 Đa thức ( Đề trắc nghiệm và tự luận)

01 Đề bài:

 ĐỀ 2

I. Phần trắc nghiệm (4 điểm)

(Chọn chữ cái trước câu trả lời đúng nhất.)

Câu 1: Cho các biểu thức dưới đây (a là hằng số). Có bao nhiêu đa thức trong các biểu thức trên? 

$3x+7+\frac{3}{x}; \frac{-1}{3}x^{2}y(1+x+2y); 3x^{2}+6x+1$; $\frac{x^{2}-2z+a}{3x+1}$

• A. 4
• B. 3
• C. 2
• D. 1

Câu 2: Chọn câu trả lời đúng nhất

• A. Mỗi đa thức được coi là một đơn thức
• B. Mỗi đơn thức được coi là một đa thức
• C.  Cả A, B đều đúng
• D. Cả A, B đều sai

Câu 3: Cho $A = 4x^{4} + 2y^{2} x-3z^{3} + 5$ và $B = -4z^{3} + 8 + 3y^{2} x-5x^{4}$. Tính A - B

• A. $-9x^{4} - y^{2}x + z^{3} - 3$
• B. $-9x^{4} - y^{2}x - z^{3} - 3$
• C. $9x^{4} - y^{2}x + z^{3} - 3$
• D. $9x^{4} - y^{2}x - z^{3} - 3$

Câu 4: Thu gọn và tìm bậc của đa thức $12xyz-3x^{5} + y^{4} + 3xyz + 2x^{5}$ ta được

• A. Kết quả là đa thức $-x^{5} - 15xyz + y^{4}$ có bậc là 4
• B. Kết quả là đa thức $-x^{5} + 15xyz + y^{4}$ có bậc là 4
• C. Kết quả là đa thức $- 2x^{5} + 15xyz + y^{4}$ có bậc là 4
• D. Kết quả là đa thức $-x^{5} + 15xyz + y^{4}$ có bậc là 5

II. Phần tự luận (6 điểm)

Câu 1: Tìm bậc của đa thức sau:

a) $ax^{3}+2xy-5$ (a là hằng số)

b) $ax^{2}+x^{2}=1$

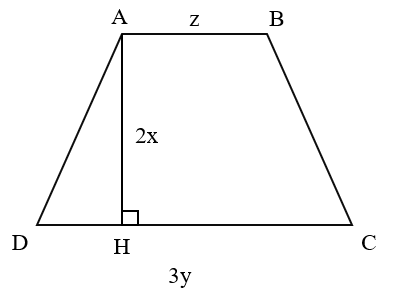
Câu 2: Tìm đa thức biểu thị diện tích hình thang và tính diện tích hình thang đó biết $x = 1; y = 1; z = 1$

02 Bài giải: