Bài tập dạng vectơ
Dạng 7: Vectơ
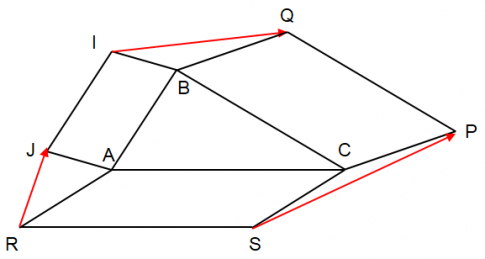
Bài tập 1: Cho tam giác ABC. Vẽ bên ngoài tam giác các hình bình hành ABIJ, BCPQ, CARS. Chứng minh $\vec{RJ}+\vec{IQ}+\vec{PS}=\vec{0}$.
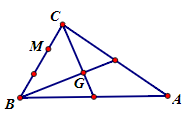
Bài tập 2: Cho tam giác ABC có trọng tâm G. Gọi M là điểm thuộc BC sao cho $\vec{BM}=2\vec{MC}$. Chứng minh:
a) $\vec{AB}+2\vec{AC}=3\vec{AM}$
b) $\vec{MA}+\vec{MB}+\vec{MC}=3\vec{MG}$
Bài tập 1:
Ta có: $\vec{RJ}+\vec{IQ}+\vec{PS}$
$=\vec{RA}+\vec{AJ}+\vec{IB}+\vec{BQ}+\vec{PC}+\vec{CS}$
$=(\vec{RA}+\vec{CS})+(\vec{AJ}+\vec{IB})+(\vec{BQ}+\vec{PC})$
$=\vec{0}$
Bài tập 2:
a) Ta có: $\vec{AB}+2\vec{AC}$
$=\vec{AM}+\vec{MB}+2(\vec{AM}+\vec{MC})$
$=\vec{AM}+\vec{MB}+2\vec{AM}+2\vec{MC}$
$=3\vec{AM}+\vec{MB}+2\vec{MC}$
Do $\vec{BM}=2\vec{MC}$ nên ta có:
$\vec{AB}+2\vec{AC}=3\vec{AM}+\vec{MB}+\vec{BM}=3\vec{AM}$
b) Ta có: $\vec{MA}+\vec{MB}+\vec{MC}$
$=\vec{MG}+\vec{GA}+\vec{MG}+\vec{GB}+\vec{MG}+\vec{GC}$
$=3\vec{MG}+\vec{GA}+\vec{GB}+\vec{GC}$
Do G là trọng tâm tam giác ABC nên $\vec{GA}+\vec{GB}+\vec{GC}=\vec{0}$
Do đó: $\vec{MA}+\vec{MB}+\vec{MC}=3\vec{MG}$
Xem toàn bộ: Đề cương ôn tập Toán 10 cánh diều học kì 1

Bình luận