Bài tập dạng dấu của tam thức bậc hai

Bài tập 1: 

a) Ta có: $-x^{2}+x-1$ vô nghiệm

$6x^{2}-5x+1=0$ $\Leftrightarrow $ $x=\frac{1}{2}$ hoặc $x=\frac{1}{3}$

Bảng xét dấu:

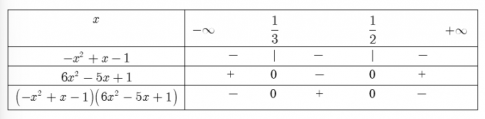
Vậy biểu thức đã cho dương khi và chỉ khi $x\in (\frac{1}{3};\frac{1}{2})$; âm khi và chỉ khi $x\in (-\infty ;\frac{1}{3})\cup (\frac{1}{2};+\infty )$

b) Ta có: $x^{2}-x-2=0$ có hai nghiệm phân biệt là x = -1; x = 2

$-x^{2}+3x+4=0$ có hai nghiệm phân biệt là x = -1; x = 4

Bảng xét dấu:

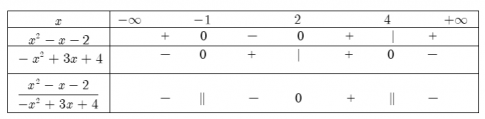
Vậy biểu thức đã cho dương khi và chỉ khi $x\in (2;4)$; âm khi và chỉ khi $x\in (-\infty ;-1)\cup (-1;2)\cup (4;+\infty )$

Bài tập 2: 

Biểu thức g(x) luôn dương

$\Leftrightarrow \sqrt{x^{2}-x+m}-1>0\Leftrightarrow \sqrt{x^{2}-x+m}>1\Leftrightarrow x^{2}-x+m-1>0$

$\forall x\Leftrightarrow \begin{cases}a& = 1>0\\ \Delta & = 5-4m<0\end{cases}\Leftrightarrow m> \frac{5}{4}$

Vậy $m> \frac{5}{4}$ thì g(x) luôn dương.