Bài tập dạng bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Bài tập 1: 

Tập xác định: D = $\mathbb{R}$

Ta có: $\frac{3x+1}{2}-\frac{x-2}{3}<\frac{1-2x}{4}$

$\Leftrightarrow \frac{6(3x+1)-4(x-2)}{12}<\frac{3(1-2x)}{12}$

$\Leftrightarrow 6(3x+1)-4(x-2)<3(1-2x)$

$\Leftrightarrow 18x+6-4x+8<3-6x$

$\Leftrightarrow 20x<-11$

$\Leftrightarrow x<-\frac{11}{20}$

Vậy tập nghiệm của bất phương trình là S = $(-\infty ;-\frac{11}{20})$

Bài tập 2: 

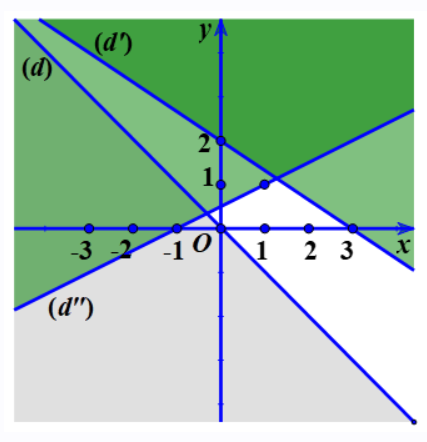
Vẽ các đường thẳng (d): x + y = 0, (d'): 2x - 3y + 6 = 0, (d''): x - 2y + 1 = 0 trên mặt phẳng tọa độ Oxy.

Xét điểm O(0;0), thấy (0;0) là nghiệm của bất phương trình 2x - 3y + 6 > 0 và x - 2y + 1 $\geq $ 0.

Do đó: O(0;0) thuộc miền nghiệm của bất phương trình 2x - 3y + 6 > 0 và x - 2y + 1 $\geq $ 0.

Xét điểm M(1;0) ta thấy (1;0) là nghiệm của bất phương trình x + y > 0. Do đó M(1;0) thuộc miền nghiệm của bất phương trình x + y > 0.

Vậy miền nghiệm cần tìm là phần mặt phẳng không tô màu trên hình vẽ và kể cả đường thẳng (d'')