Bài tập dạng quan hệ giữa các yếu tố trong một tam giác
PHẦN HÌNH HỌC
Dạng 1: Quan hệ giữa các yếu tố trong một tam giác
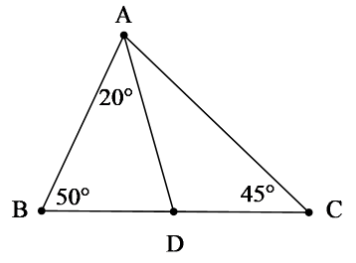
Bài tập 1: Tính số đo $\widehat{CAD}$ trong hình vẽ dưới đây:
Bài tập 2: Bộ ba dộ dài sau đây có thể là ba cạnh của một tam giác?
a) 3 cm, 4 cm, 5 cm
b) 2 m, 3 m, 6m
Bài tập 3: Cho hai điểm A và B nằm về hai phía của đường thẳng d. Tìm điểm C thuộc đường thẳng d sao cho tổng AC + CB nhỏ nhất
Bài tập 1:
$\widehat{ADC}$ là góc ngoài tại đỉnh D của tam giác ABD nên ta áp dụng định lý góc ngoài của tam giác ABD có: $\widehat{ADC}=\widehat{BAD}+\widehat{ABD}=20^{o}+50^{o}=70^{o}$
Áp dụng định lý tổng ba góc trong tam giác ADC có:
$\widehat{CAD}+\widehat{ACD}+\widehat{ADC}=180^{o}$
$\Rightarrow \widehat{CAD}=180^{o}-45^{o}-70^{o}=65^{o}$
Bài tập 2:
a) Ta có 5 cm là số lớn nhất mà 3 + 4 > 5 nên bộ ba cạnh 3 cm, 4 cm, 5 cm lập thành một tam giác
b) Ta có 2 + 3 < 6 nên bộ ba cạnh 2 m, 3 m, 6 m không lập thành một tam giác
Bài tập 3:
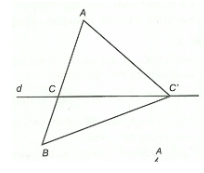
Giả sử C là giao điểm của đoạn thẳng AB với đường thẳng d
Vì C nằm giữa A và B nên ta có AC + CB = AB
Lấy điểm C' bất kì trên d ($C' \neq C$)
Nối AC', BC'
Sử dụng bất đẳng thức tam giác vào $\Delta ABC'$ ta có: AC' + BC' > AB
Suy ra AC' + BC' > AC + CB
Vậy C là điểm cẩn tìm
Xem toàn bộ: Đề cương ôn tập Toán 7 cánh diều học kì 2

Bình luận