Bài tập dạng Đường trung trực - Đường trung tuyến - Đường cao - Đường phân giác của tam giác

Bài tập 1: Vì Bx // AC nên $\widehat{CBx}=\widehat{BCE}$ (so le trong).

Gọi M là trung điểm của BC.

Ta có $\Delta BMD= \Delta CME$ (c.g.c).

Suy ra MD = ME (1) và $\widehat{BMD}=\widehat{CME}$

Ta có $\widehat{BME}+\widehat{CME}=180^{o}$ (kề bù)

Do đó $\widehat{BME}+\widehat{CME}=180^{o}$ nên D, M, E thẳng hàng. (2)

Từ (1) và (2) suy ra M là trung điểm của DE.

$\Delta ABC$ và $\Delta ADE$ chung đỉnh A, chung đường trung tuyến AM nên trọng tâm G của hai tam giác này trùng nhau.

Bài tập 2: 

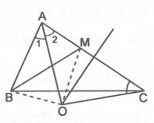
Điểm O nằm trên đường trung trực của AC nên OA = OC

Do đó $\Delta OAC$ cân tại O, suy ra $\widehat{A_{2}}=\widehat{OCA}$

Mặt khác $\hat{A_{1}}=\hat{A_{2}}$ nên $\hat{A_{1}}=\widehat{OCA}$

$\Delta ABO$ và $\Delta CMO$ có: AB = CM, $\hat{A_{1}}=\widehat{OCA}$, OA = OC nên $\Delta ABO = \Delta CMO$ (c.g.c)

Suy ra OB = OM

Hay O nằm trên đường trung trực của BM

Bài tập 3: 

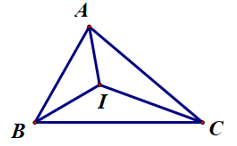
$\Delta ABC$ có: $\widehat{ACB}+\widehat{ABC}+\widehat{BAC} = 180^{o}$ (định lí tổng ba góc của tam giác)

Suy ra $\widehat{ACB} = 180^{o}-60^{o}-80^{o}=40^{o}$

Ta có I là điểm nằm trong tam giác và cách đều ba cạnh của $\Delta ABC$

Ta suy ra I là giao điểm của ba đường phân giác của $\Delta ABC$

Do đó $\widehat{ICA}=\frac{1}{2}.\widehat{ACB}=\frac{1}{2}.40^{o}=20^{o}$