TRẮC NGHIỆM

Câu 1: Trong không gian với hệ trục tọa độ cho hai điểm , . Tính độ dài đoạn thẳng .

• A. .                              

• B. .
• C. .                                
• D. .

Câu 2: Trong không gian với hệ tọa độ , cho hai điểm , . Mặt cầu nhận làm đường kính có phương trình là

• A. .                          

• B. .

• C. .                            
• D. .

Câu 3: Trong không gian , cho đường thẳng và mặt phẳng . Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng , đồng thời vuông góc và cắt đường thẳng ?

• A. .                                             

• B. .

• C. .                                        
• D. .

Câu 4: Họ các nguyên hàm của hàm số là 

• A. .
• B. .
• C. .

• D. .

Câu 5: Nguyên hàm của hàm số là

• A. .

• B. . 
• C. .
• D. .

Câu 6: Biết , với là các số nguyên. Tính .

• A. .
• B. .

• C. .

• D. .

Câu 7: Giả sử là hàm liên tục trên và là ba số bất kì trên khoảng . Khẳng định nào sau đây sai?

• A. .
• B. .

• C. .

• D. .

Câu 8: Cho với là các số nguyên. Mệnh đề nào sau đây đúng?

• A. .
• B. .

• C. .

• D. .

Câu 9: Thể tích của khối tròn xoay khi quay hình phẳng giới hạn bởi các đường , trục và hai đường thẳng quanh trục hoành được tính bởi công thức nào sau đây?

• A. .
• B. .

• C. .

• D.

Câu 10: Cho đồ thị hàm số Diện tích của hình phẳng là

• A. .

• B. .

• C. .
• D.

Câu 11: Trong không gian , cho ba điểm và . Vectơ pháp tuyến của mặt phẳng là

• A. .

• B. .

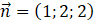• C. .
• D. .

Câu 12: Trong không gian , cho ba điểm . Phương trình mặt phẳng là

• A. .

• B. .

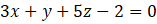• C. .
• D. .

Câu 13: Cho mặt phẳng . Viết phương trình mặt phẳng song song với mặt phẳng , đồng thời cắt trục lần lượt tại các điểm sao cho .

• A. .

• B. .
• C. .
• D. .

Câu 14: Trong không gian , phương trình đường thẳng đi qua điểm

• A. .

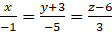• B. .
• C. .
• D. .

Câu 15: Trong không gian tọa độ , cho ba điểm . Viết phương trình đường thẳng qua và song song với .

• A. .

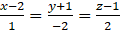• B. .
• C. .
• D. .

Câu 16: Trong không gian , cho hai đường thẳng và và mặt phẳng . Đường thẳng vuông góc với , cắt và có phương trình là

• A. .

• B. .

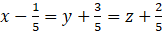• C. .
• D. .

Câu 17: Cho hai mặt phẳng và . Có bao nhiêu giá trị của sao cho góc giữa hai mặt phẳng và bằng .

• A. 0.
• B. 2.
• C. 3.

• D. 4.

Câu 18: Trong không gian với hệ trục tọa độ , gọi là mặt phẳng chứa đường thẳng và tạo với trục góc có số đo lớn nhất. Điểm nào sau đây thuộc mp ?

• A. .
• B. .

• C. .

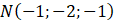• D. .

Câu 19: Phương trình mặt cầu tâm và bán kính là

• A. .

• B. .

• C. .
• D. .

Câu 20: Trong không gian , cho hai điểm và . Phương trình mặt cầu có đường kính là

• A. .

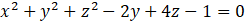• B. .
• C. .
• D. .

Câu 21: Lớp Toán Sư Phạm có 95 sinh viên, trong đó có 40 nam và 55 nữ. Trong kỳ thi môn Xác suất thống kê có 23 sinh viên đạt điểm giỏi (trong đó có 12 nam và 11 nữ). Gọi tên ngẫu nhiên một sinh viên trong danh sách lớp. Tính xác suất gọi được sinh viên đạt điểm giỏi môn Xác suất thống kê, biết rằng sinh viên đó là nữ.

• A. .

• B. .
• C. .
• D. .

Câu 22: Một nhà máy sản xuất hai loại sản phẩm A và B. Tỉ lệ sản phẩm A là 30%, và tỉ lệ sản phẩm B là 70%. Xác suất một sản phẩm A bị lỗi là 2%, và xác suất một sản phẩm B bị lỗi là 5%. Một sản phẩm được chọn ngẫu nhiên từ nhà máy và được phát hiện là bị lỗi. Tính xác suất sản phẩm đó là sản phẩm A.

• A. 0,25.

• B. 0,146.

• C. 0,35.
• D. 0,4.

Câu 23: Trong không gian , cho hai điểm . Từ điểm kẻ được bao nhiêu đường thẳng cắt mặt cầu đường kính tại hai điểm thỏa mãn ?

• A. 0.
• B. 2.

• C. 1.

• D. Vô số.

Câu 24: Cho hàm số thỏa mãn với mọi dương. Biết . Giá trị bằng

• A. .

• B. .

• C. .
• D. .

Câu 25: Cho hàm số liên tục trên và thỏa mãn và . Tính .

• A. 0.
• B. 1.
• C. 4.

• D. 8.