PHƯƠNG TRÌNH MẶT PHẲNG

I. VECTOR PHÁP TUYẾN. CẶP VECTOR CHỈ PHƯƠNG CỦA MẶT PHẲNG

1. Vector pháp tuyến

Hoạt động 1 trang 50 sgk toán 12 tập 2 cd

Cho hình hộp chữ nhật ABCD.A’B’C’D’ (Hình 2). Giá của vector có vuông góc với mặt phẳng ABCD hay không?

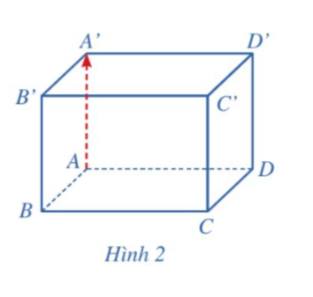
Giải nhanh:

Vector vuông với mặt phẳng ABCD

Luyện tập-vận dụng 1 trang 51 sgk toán 12 tập 2 cd

Trong không gian với hệ tọa độ Oxyz, hãy chỉ ra một vectơ pháp tuyến của:

a) Mặt phẳng (Oyz);

b) Mặt phẳng (Ozx).

Giải nhanh:

a) =(1;0;0) 

b) =(0;1;0) 

2. Cặp vector chỉ phương

Hoạt động 2 trang 51 sgk toán 12 tập 2 cd

Cho hình hộp ABCD.A'B'C'D'. Cho biết hai vectơ có cùng phương hay không. Nhận xét về vị trí tương đối giữa giá của mỗi vectơ  và mặt phẳng (ABCD) (Hình 5).

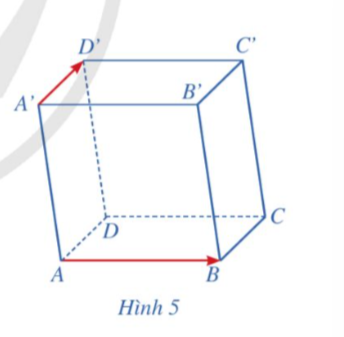
Giải nhanh:

Vector  nằm trong mặt phẳng ABCD

Vector  nằm ngoài mặt phẳng ABCD và song song với mặt phẳng.

Luyện tập-vận dụng 2 trang 51 sgk toán 12 tập 2 cd

Trong không gian với hệ tọa độ Oxyz, hãy chỉ ra một cặp vectơ chỉ phương của mỗi mặt phẳng (Oxy), (Oyz), (Ozx).

Giải nhanh:

Mặt phẳng (Oxy) là mặt phẳng đi qua trục Ox, Oy và vuông góc với trục Oz. Do đó, hai vectơ chỉ phương của mặt phẳng (Oxy) là:

- i = (1, 0, 0)

- j = (0, 1, 0)

Mặt phẳng (Oyz) là mặt phẳng đi qua trục Oy, Oz và vuông góc với trục Ox. Do đó, hai vectơ chỉ phương của mặt phẳng (Oyz) là:

- j = (0, 1, 0)

- k = (0, 0, 1)

Mặt phẳng (Ozx) là mặt phẳng đi qua trục Ox, Oz và vuông góc với trục Oy. Do đó, hai vectơ chỉ phương của mặt phẳng (Ozx) là:

- i = (1, 0, 0)

- k = (0, 0, 1)

3. Xác định vector pháp tuyến của mặt phẳng khi biết cặp vector chỉ phương 

Hoạt động 3 trang 52 sgk toán 12 tập 2 cd

Cho cặp vectơ chỉ phương a=(1;0;1) và b=(2;1;0) của mặt phẳng (P).

a) Hãy chỉ ra tọa độ của một vectơ n(n khác 0) vuông góc với cả hai vectơ a và b (Hình 6)

b) Vectơ n có là vectơ pháp tuyến của mặt phẳng (P) hay không?

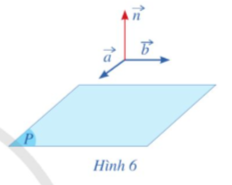
Giải nhanh:

a)

b) Vectơ pháp tuyến của mặt phẳng (P) là vectơ vuông góc với vectơ chỉ phương của mặt phẳng. Do đó, vectơ là vectơ pháp tuyến của mặt phẳng (P).

Luyện tập-vận dụng 3 trang 52 sgk toán 12 tập 2 cd

Trong Ví dụ 3, vectơ   có là vectơ pháp tuyến của mặt phẳng (P) hay không? Vì sao?

Giải nhanh:

Ta có:

Do đó, cũng là một vectơ pháp tuyến của mặt phẳng (P).

II. Phương trình tổng quát của mặt phẳng

Hoạt động 4 trang 52 sgk toán 12 tập 2 cd

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm A(1;-1;2) và có vectơ pháp tuyến là Giả sử (M(x;y;z)) là một điểm tuỳ ý thuộc mặt phẳng (P) (Hình 7).

a) Tính tích vô hướng theo x, y, z.

b) Toạ độ (x; y, z) của điểm M có thoả mãn phương trình: hay không?

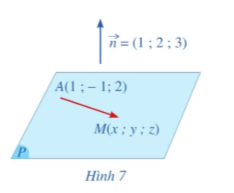
Giải nhanh:

a) Ta có:

là vectơ pháp tuyến của mặt phẳng (P).

A(1;-1;2) là một điểm thuộc mặt phẳng (P).

M(x;y;z) là một điểm tuỳ ý thuộc mặt phẳng (P).

Tính vec-tơ :

Tính tích vô hướng:

Vậy, tích vô hướng theo x, y, z là x + 2y + 3z – 5.

b) Vì  ,là vector pháp tuyến của (P)

Vậy toạ độ (x; y, z) của điểm M có thoả mãn phương trình:

Luyện tập vận dụng 4 trang 54 sgk toán 12 tập 2 cd

Chỉ ra một vectơ pháp tuyến của mỗi mặt phẳng sau:

a) (P): x-y=0;

b) (Q): z-2=0

Giải nhanh:

a) Mặt phẳng (P):

Như vậy mặt phẳng P nhận   làm vector pháp tuyến

b) Mặt phẳng (Q):

Như vậy mặt phẳng P nhận   làm vector pháp tuyến

III. LẬP PHƯƠNG TRÌNH TỔNG QUÁT CỦA MẶT PHẲNG BIẾT MỘT SỐ ĐIỀU KIỆN

1. Lập phương trình tổng quát của mặt phẳng đi qua 1 điểm và biết vector pháp tuyến 

Hoạt động 5 trang 54 sgk toán 12 tập 2 cd

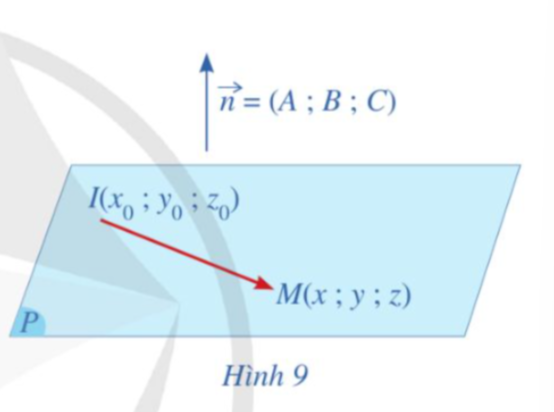
Cho mặt phẳng (P) đi qua điểm có   là vectơ pháp tuyến. Giả sử M(x;y;z) là một điểm bất kì thuộc mặt phẳng (P) (Hình 9).

a) Tính tích vô hướng  

b) Hãy biểu diễn theo và A,B,C

Giải nhanh:

a) Ta có:

Vector là vectơ từ điểm đến điểm trên mặt phẳng (P). Vector này có phương trình:

Tích vô hướng của hai vectơ và :

b)

Luyện tập-vận dụng 5 trang 54 sgk toán 12 tập 2 cd

Cho hai điểm M(2; 1; 0) và N(3; 0; 1). Lập phương trình mặt phẳng trung trực của đoạn thẳng MN.

Giải nhanh:

Vectơ chỉ phương của đường thẳng MN là  

 Trung điểm của đoạn thẳng MN là điểm P có tọa độ:

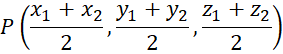
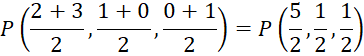
Mặt phẳng trung trực của đoạn thẳng MN là mặt phẳng vuông góc với vectơ và đi qua trung điểm P.

Phương trình tổng quát của một mặt phẳng là:

   Trong đó, là vectơ pháp tuyến của mặt phẳng. Ở đây, vectơ pháp tuyến chính là . Ta có phương trình mặt phẳng:

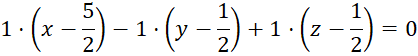
Phương trình đi qua trung điểm :

Vậy phương trình mặt phẳng là:

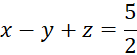
2. Lập phương trình tổng quát của mặt phẳng đi qua 1 điểm và biết được cặp vector chỉ phương

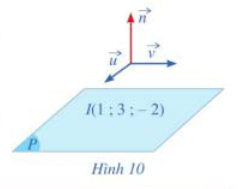
Hoạt động 6 trang 55 sgk toán 12 tập 2 cd

Cho mặt phẳng (P) đi qua điểm I(1:3:-2) có cặp vectơ chỉ phương là và

a) Hãy chỉ ra một vectơ pháp tuyến của mặt phẳng (P).

b) Lập phương trình mặt phẳng (P) đi qua điểm (1; 3;-2), biết vectơ pháp tuyến

Giải nhanh:

a) Vectơ pháp tuyến của mặt phẳng (P) là tích có hướng của hai vectơ chỉ phương và

Vậy một vectơ pháp tuyến của mặt phẳng (P) là

b)

Phương trình mặt phẳng (P) đi qua điểm và có vectơ pháp tuyến là:

Khai triển phương trình, ta được:

Như vậy phương trình mặt phẳng (P) là

Luyện tập-vận dụng 6 trang 55 sgk toán 12 tập 2 cd

 Cho mặt phẳng (P) đi qua điểm (). Lập phương trình mặt phẳng (P), biết mặt phẳng đó:

a) Vuông góc với trục Ox,

b) Vuông góc với trục Oy;

c) Vuông góc với trục Oz.

Giải nhanh:

a)

b)

c)

 Hoạt động 7 trang 55 sgk toán 12 tập 2 cd

Cho ba điểm cùng thuộc mặt phẳng (P) (Hình 11).

a) Tìm toạ độ của các vectơ Từ đó hãy chứng tỏ rằng ba điểm H, I, K không thẳng hàng.

b) Lập phương trình mặt phẳng (P) đi qua điểm (H(-1;1;2) biết cặp vectơ chỉ phương là

Giải nhanh:

a) Tọa độ của vectơ

Tọa độ của vectơ

Chúng ta kiểm tra xem có tồn tại số k nào sao cho:

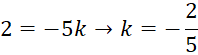
Do các phương trình mâu thuẫn với nhau, không tồn tại số k nào thỏa mãn cả ba phương trình, do đó hai vectơ và không cùng phương. Vì vậy, ba điểm H, I, K không thẳng hàng.

b) Phương trình mặt phẳng (P) có dạng:

Trong đó, (a, b, c) là tọa độ của một vectơ pháp tuyến của mặt phẳng, được xác định bằng tích có hướng của hai vectơ chỉ phương và

Do đó, phương trình mặt phẳng có dạng:

Vậy phương trình mặt phẳng (P) là:

Luyện tập-vận dụng 7 trang 56 sgk toán 12 tập 2 cd

Lập phương trình mặt phẳng đi qua ba điểm M(1; 2; 1), N(0; 3; 2) và P(-1; 0; 0)

Giải nhanh:

Để lập phương trình mặt phẳng đi qua ba điểm và chúng ta sẽ thực hiện các bước sau:

 Tìm tọa độ của các vectơ và

Tọa độ của vectơ

Tọa độ của vectơ

Tìm tọa độ của vectơ pháp tuyến của mặt phẳng

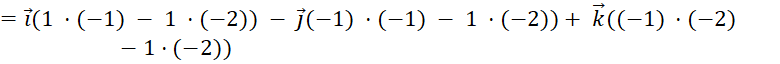
Phương trình mặt phẳng có dạng:

Trong đó (a, b, c) là tọa độ của vectơ pháp tuyến và là tọa độ của một điểm nằm trên mặt phẳng, ví dụ như điểm

Vậy phương trình mặt phẳng đi qua ba điểm và là:

Phương trình mặt phẳng đi qua ba điểm A(2, 0, 0), B(0, 3, 0), và C(0, 0, 4) là:

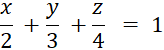
IV. ĐIỀU KIỆN SONG SONG, VUÔNG GÓC CỦA 2 MẶT PHẲNG

1. Điều kiện song song của 2 mặt phẳng

Hoạt động 8 trang 57 sgk toán 12 tập 2 cd

 Cho mặt phẳng (P₁):

Và mặt phẳng (P₂):

a) Gọi lần lượt là vectơ pháp tuyến của hai mặt phẳng (Hình 14). Tìm liên hệ giữa và

b) Tìm hệ số tự do D₁, D₂ lần lượt của 2 phương trình (1), (2). So sánh D₁ và 2D₂

c) Nêu vị trí tương đối của 2 mặt phẳng (P₁), (P₂).

Giải nhanh:

a)

b)

c) Hai mặt phẳng này song song và không trùng nhau.

Luyện tập-vận dụng 9 trang 58 sgk toán 12 tập 2 cd

Chứng minh rằng các mặt phẳng

(P): (x-m=0)

(Q): (y-m=0)

(R): (z-m=0)

lần lượt song song với các mặt phẳng (Oyz), (Ozx), (Oxy).

Giải nhanh:

Xét mặt phẳng (P) và (Oyz) có phương trình lần lượt là 

Ta thấy 2 mặt phẳng đều có vector chỉ phương . Tuy nhiên hệ số của 2 phương trình khác nhau . Như vậy (P)//(Oyz)

Xét mặt phẳng (Q) và (Oxz) có phương trình lần lượt là 

Ta thấy 2 mặt phẳng đều có vector chỉ phương . Tuy nhiên hệ số của 2 phương trình khác nhau . Như vậy (Q)//(Oxz)

Xét mặt phẳng (R) và (Oxy) có phương trình lần lượt là 

Ta thấy 2 mặt phẳng đều có vector chỉ phương . Tuy nhiên hệ số của 2 phương trình khác nhau . Như vậy (R)//(Oxy)

2. Điều kiện vuông góc của 2 mặt phẳng

Hoạt động 9 trang 58 sgk toán 12 tập 2 cd

Cho mặt phẳng có phương trình tổng quát là:

và mặt phẳng có phương trình tổng quát là:

Gọi lần lượt là vectơ pháp tuyến của hai mặt phẳng Hai vectơ có vuông góc với nhau hay không?

Giải nhanh:

Xét tích vô hướng:

=> vectơ vuông góc với nhau.

Luyện tập-vận dụng 10 trang 59 sgk toán 12 tập 2 cd

Chứng minh rằng hai mặt phẳng (Ozx) và (P): x + 2z - 3 = 0 vuông góc với nhau.

Giải nhanh:

Hai mặt phẳng (Ozx) và (P): x + 2z - 3 = 0 vuông góc với nhau.

V. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG

Hoạt động 10 trang 59 sgk toán 12 tập 2 cd

Cho mặt phẳng (P) có phương trình tổng quát là với là vecto pháp tuyến. Cho điểm Gọi là hình chiếu vuông góc của điểm M trên mặt phẳng (P)

a) Tính toạ độ của theo

b) Nêu nhận xét về phương của hai vectơ           

Từ đó, hãy suy ra rằng

=

c) Tính các độ dài theo A, B, C, D. Từ đó, hãy nêu công thức tính khoảng cách từ điểm M₀(2;3;4) đến mặt phẳng (P).

Giải nhanh:

 a) Tính tọa độ của theo

Gọi là hình chiếu vuông góc của điểm trên mặt phẳng (P). Tọa độ của là:

b)  Vì H  là hình chiếu vuông góc của trên mặt phẳng (P), nên vectơ phải song song với vectơ pháp tuyến .

Vì 2 vector song song nên:

=>

Do H nằm trên mặt phẳng (P), ta có phương trình của mặt phẳng (P):

=>

Vậy:

c) 

Độ dài của

Độ dài của chính là khoảng cách từ M₀ đến mặt phẳng (P)

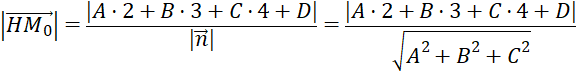
Do đó, khoảng cách từ là khoảng cách từ M₀ đến mặt phẳng (P) là:

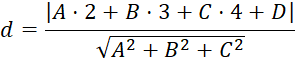
Công thức tính khoảng từ điểm M₀(2;3;4) đến mặt phẳng (P):

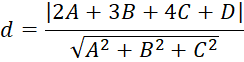
Hoạt động 11 trang 60 sgk toán 12 tập 2 cd

Chứng minh rằng khoảng cách từ điểm M(a, b, c) đến các mặt phẳng (Oyz), (Ozx), (Oxy) lần lượt bằng |a|,|b|,|c|

Giải nhanh:

•  Khoảng cách từ điểm M đến mặt phẳng (Oyz):

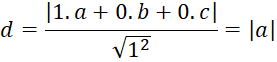
Khoảng cách từ điểm M đến mặt phẳng (Ozx):

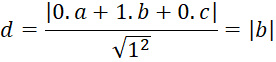
• Khoảng cách từ điểm M đến mặt phẳng (Oxy):

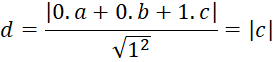
Luyện tập-vận dụng 12 trang 60 sgk toán 12 tập 2 cd

Cho mặt phẳng và mặt phẳng

a) Chứng minh rằng:

b) Tính khoảng cách giữa hai mặt phẳng song song,

Giải nhanh:

a) Vecto pháp tuyến của mặt phẳng

Vecto pháp tuyến của mặt phẳng

Ta có:

Vậy,  

b) Chọn điểm là 1 điểm thuộc P₁

Khoảng cách giữa M đến (P₂):

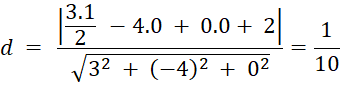
BÀI TẬP

Bài 1 trang 63 sgk toán 12 tập 2 cd

 Phương trình nào sau đây là phương trình tổng quát của mặt phẳng?

Giải nhanh:

Bài 2 trang 63 sgk toán 12 tập 2 cd

Mặt phẳng x + 2y - 3z + 4 = 0 có một vectơ pháp tuyến là:

A. = (2; -3; 4).

B. = (1; 2; 3).

C. = (1; 2; -3).

D. = (1; 2; 4).

Giải nhanh:

C. = (1; 2; -3).

Bài 3 trang 63 sgk toán 12 tập 2 cd

Lập phương trình mặt phẳng (P) đi qua điểm I(3;-4;5) và nhận làm vectơ pháp tuyến.

Giải nhanh:

Bài 4 trang 63 sgk toán 12 tập 2 cd

Lập phương trình mặt phẳng (P) đi qua điểm (K(-1;2;3) và nhận hai vectơ và làm cặp vectơ chỉ phương.

Giải nhanh:

Bài 5 trang 63 sgk toán 12 tập 2 cd

Lập phương trình mặt phẳng (P) đi qua:

a) Điểm I (3; −4; 1) và vuông góc với trục Ox,

b) Điểm K(-2;4;-1) và song song với mặt phẳng (Ozx);

c) Điểm K(-2;4;-1) và song song với mặt phẳng (Q): 3x+7y+10z+1=0.

Giải nhanh: 

a)  x = 3 

b)  y = 4 

c)

Bài 6 trang 63 sgk toán 12 tập 2 cd

 Lập phương trình mặt phẳng (P) đi qua ba điểm A(1; 1; 1), B(0; 4; 0), C(2; 2; 0).

Giải nhanh:

Chọn hai vectơ chỉ phương của mặt phẳng (P) là:

Vectơ pháp tuyến của mặt phẳng (P) là:

Chọn điểm A(1; 1; 1) để viết phương trình mặt phẳng (P).

Bài 7 trang 63 sgk toán 12 tập 2 cd

 Lập phương trình mặt phẳng theo đoạn chắn của mặt phẳng (P), biết (P) đi qua ba điểm A(5; 0; 0), B(0; 3; 0), C(0; 0; 6).

Giải nhanh: 

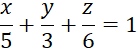
Bài 8 trang 64 sgk toán 12 tập 2 cd

Cho hai mặt phẳng

a) Chứng minh rằng

b) Tính khoảng cách giữa hai mặt phẳng song song

Giải nhanh:

a) Ta có:

- Vector pháp tuyến của là

- Vector pháp tuyến của là

Xét tỉ lệ giữa các thành phần của 2 vector:

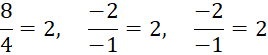
Tất cả các tỉ lệ đều bằng nhau, nghĩa là:

Do đó, hai vector pháp tuyến và là cùng phương. Vì vậy, hai mặt phẳng và là song song.

b) Chọn điểm

Khoảng cách giữa 2 mặt phẳng song song:

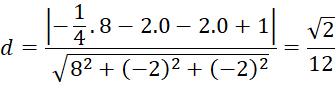
Bài 9 trang 64 sgk toán 12 tập 2 cd

a) Cho hai mặt phẳng Chứng minh rằng

b) Cho mặt phẳng và điểm M(1; 1; -6). Tính khoảng cách từ điểm M đến mặt phẳng (P)

Giải nhanh:

a) Ta có:

Vector pháp tuyến của mặt phẳng (P₁):

Vector pháp tuyến của mặt phẳng (P₂):

Để thì

Ta có 

Vậy  

b) Khoảng cách từ điểm M đến mặt phẳng (P):

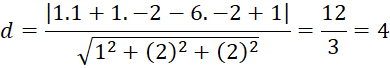
Bài 10 trang 64 sgk toán 12 tập 2 cd

Trong không gian với hệ toạ độ Oxyz, cho hình chóp S.OBCD có đáy là hình chữ nhật và các điểm O(0;0;0), B(2; 0; 0), D(0; 3; 0), S(0; 0; 4) (Hình 19).

a) Tìm toạ độ điểm C.

b) Viết phương trình mặt phẳng (SBD).

c) Tính khoảng cách từ điểm C đến mặt phẳng (SBD).

Giải nhanh:

a) 

Ta có:

Vậy điểm C(2;3;0)

b) Viết phương trình mặt phẳng (SBD)

Ta có: 

Tọa độ điểm B(2;0;0)

Tọa độ điểm D(0;3;0)

Tọa độ điểm S(0;0;4)

Ba điểm S(0, 0, 4), B(2, 0, 0) và D(0, 3, 0) không thẳng hàng nên chúng xác định một mặt phẳng.

Xét các vectơ:

Tích có hướng của hai vectơ này là:

Vậy vectơ pháp tuyến của mặt phẳng là

Phương trình mặt phẳng có dạng:

Thay tọa độ điểm S(0, 0, 4) vào phương trình trên:

Vậy phương trình mặt phẳng là:

c) 

Tọa độ điểm C là (2, 3, 0). Khoảng cách từ điểm C đến mặt phẳng (SBD) là:

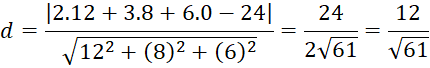
Bài 11 trang 64 sgk toán 12 tập 2 cd

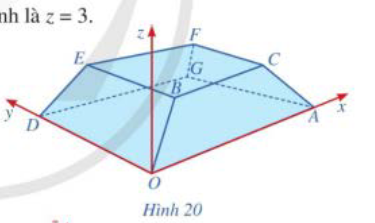
Hình 20 minh họa hình ảnh một tòa nhà trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là mét). Biết A(50; 0; 0), D(0; 20; 0), B(4k; 3k; 2k) với k > 0 và mặt phẳng (CBEF) có phương trình là z = 3.

a) Tìm tọa độ của điểm B.

b) Lập phương trình mặt phẳng (AOBC).

c) Lập phương trình mặt phẳng (DOBE).

Giải nhanh:

a)  Mặt phẳng (CBEF) có chứa điểm B có phương trình:

Thay tọa độ điểm B vào, ta có:

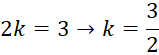
Ta có tọa độ điểm B:

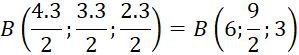
b) Mặt phẳng (AOBC) đi qua các điểm A(50; 0; 0), ,O(0,0,0)

Ta có:

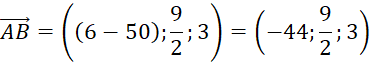
Tính vector pháp tuyến:

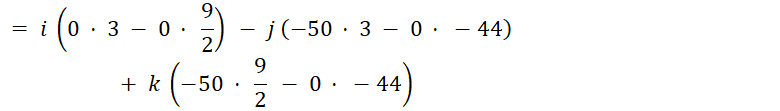
Rút gọn vector:

Phương trình mặt phẳng (AOBC) có dạng

Thay O vào phương trình, ta được:

Phương trình mặt phẳng (AOBC) là:

c) Phương trình mặt phẳng (DOBE) đi qua các điểm D(0; 20; 0), O(0,0,0) và ,

Ta có:

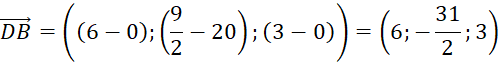
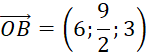
Tính vector pháp tuyến:

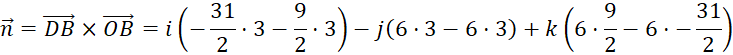
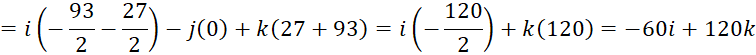
Rút gọn:

Phương trình mặt phẳng (DOBE) có dạng

Thay điểm D vào phương trình, ta được D=0.

Phương trình mặt phẳng (DOBE) có dạng

d) Vector pháp tuyến của mặt phẳng (AOBC): là:

Vector pháp tuyến của mặt phẳng (DOBE): là:

Bài 12 trang 64 sgk toán 12 tập 2 cd

Hình 21 minh họa một khu nhà đang xây dựng được gắn hệ trục tọa độ Oxyz (đơn vị trên các trục là mét). Mỗi cột bê tông có dạng hình lăng trụ tứ giác đều và tâm của mặt đáy trên lần lượt là các điểm A(2; 1; 3), B(4; 3; 3), C(6; 3; 2,5), D(4; 0; 2,8).

a) Viết phương trình mặt phẳng (ABC).

b) Bốn điểm A, B, C, D có đồng phẳng không?

Giải nhanh:

Mặt phẳng (ABC) đi qua điểm A(2; 1; 3), B(4; 3; 3), C(6; 3; 2,5).

Tính các vector

Tính vector pháp tuyến:

Phương trình mặt phẳng ABC có dạng: 

Thay điểm A vào ta có:

Vậy phương trình mặt phẳng (ABC) là::

b) Thay D(4;0;2,8) vào phương trình (ABC), ta có:

Vậy 4 điểm A,B,C,D không thẳng hàng do D không thuộc mặt phẳng (ABC)