Dễ hiểu giải Toán 12 Cánh diều bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải dễ hiểu bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số. Trình bày rất dễ hiểu, nên tiếp thu Toán 12 Cánh diều dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 4: KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
I. SƠ ĐỒ KHẢO SÁT HÀM SỐ
Hoạt động: Lập bảng biến thiên và vẽ đồ thị của hàm số ![]() .
.
Giải nhanh:
- Bảng biến thiên:
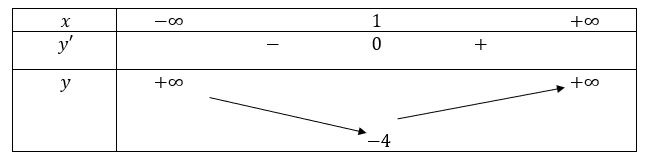
- Vẽ đồ thị hàm số

Luyện tập 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số ![]() .
.
Giải nhanh:
- Bảng biến thiên:

Đồ thị

II. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC BA
Luyện tập 2: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
Giải nhanh:
a) - Bảng biến thiên:

Đồ thị:

Vậy đồ thị hàm số ![]() được cho như hình vẽ trên
được cho như hình vẽ trên
III. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA MỘT SỐ HÀM PHÂN THỨC HỮU TỈ
Luyện tập 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số ![]() .
.
Giải nhanh:
Bảng biến thiên:

Đồ thị:

Luyện tập 4: Khảo sát sự biến thiên và vẽ đồ thị hàm số ![]() .
.
Giải nhanh:
- Bảng biến thiên:

Đồ thị:

Luyện tập 6: Khảo sát sự biến thiên và vẽ đồ thị hàm số ![]() .
.
Giải nhanh:
Bảng biến thiên:

Đồ thị
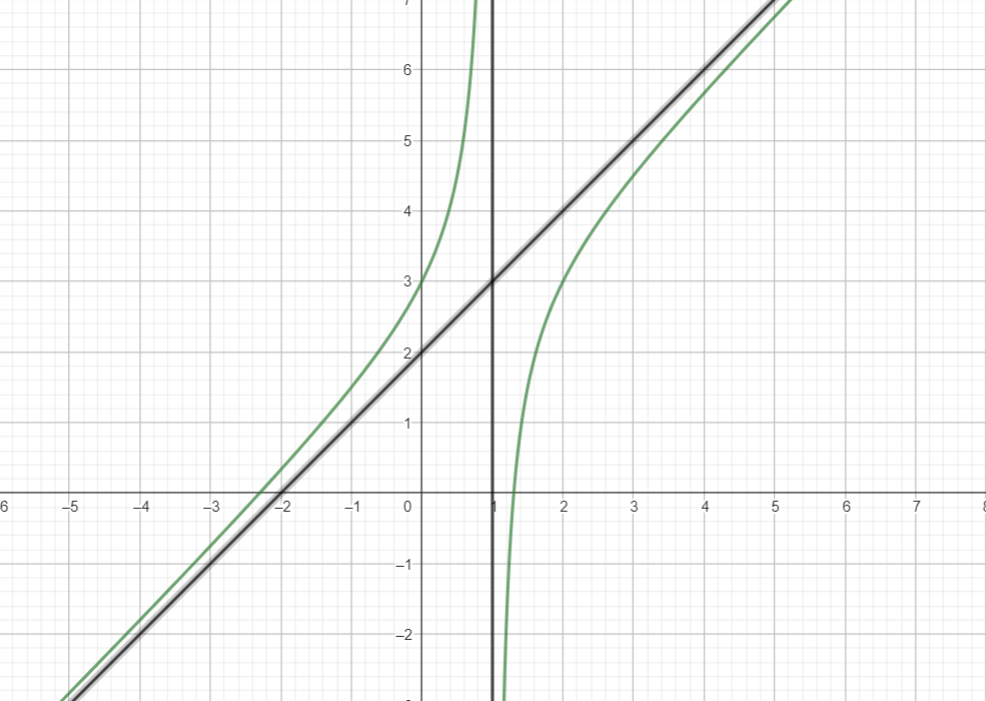
IV. ỨNG DỤNG ĐẠO HÀM VÀ KHẢO SÁT HÀM SỐ ĐỂ GIẢI QUYẾT MỘT SỐ VẤN ĐỀ LIÊN QUAN ĐẾN THỰC TIỄN
Luyện tập 7: Trong Ví dụ 9, góc dốc của con đường trên đoạn ![]() lớn nhất tại điểm nào?
lớn nhất tại điểm nào?
Giải nhanh:
Xét hàm số ![]()
Với ![]()
Ta có: ![]()
Trên đoạn ![]() ,
, ![]() khi
khi ![]()
GIẢI BÀI TẬP
Bài 1: Đồ thị hàm số ![]() là đường cong nào trong các đường cong sau?
là đường cong nào trong các đường cong sau?

Giải nhanh:
Đáp án B
Bài 2: Đường cong ở Hình 29 là đồ thị của hàm số:
 .
. .
. .
. .
.

Giải nhanh:
D. ![]()
Bài 3: Đường cong nào sau đây là đồ thị của hàm số ![]() ?
?

Giải nhanh:
Đáp án B
Bài 4: Đường cong ở Hình 30 là đồ thị của hàm số:
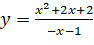 .
. .
.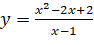 .
. .
.

Giải nhanh:
Đáp án A
Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
Giải nhanh:
a) - Bảng biến thiên:




Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
Giải nhanh:
a) Bảng biến thiên:


c) Bảng biến thiên:


e) Bảng biến thiên:


Bài 7: Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng.
Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao ![]() của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm
của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm
![]()
trong đó ![]() là thời gian tính bằng giây và
là thời gian tính bằng giây và ![]() là độ cao tính bằng kilomet (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).
là độ cao tính bằng kilomet (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).
- Tìm thời điểm
 sao cho con tài đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?
sao cho con tài đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu? - Vẽ đồ thị của hàm số
 với
với  (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km).
(đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km). - Gọi
 là vận tốc tức thời của con tàu ở thời điểm
là vận tốc tức thời của con tàu ở thời điểm  (giây) kể từ khi đốt cháy các tên lửa hãm với
(giây) kể từ khi đốt cháy các tên lửa hãm với  . Xác định hàm số
. Xác định hàm số  .
. - Vận tốc tức thời của con tàu lúc bắt đầu hãm phanh là bao nhiêu? Tại thời điểm
 (giây) là bao nhiêu?
(giây) là bao nhiêu? - Tại thời điểm
 (giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
(giây), vận tốc tức thời của con tàu vẫn giảm hay đang tăng trở lại?
Giải nhanh:
a) ![]()
Trên khoảng ![]() ,
, ![]() ↔
↔ ![]()
![]() ,
, ![]() ,
, ![]()
Do đó, ![]() tại
tại ![]()
Như vậy tại thời điểm ![]() giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.
giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.
b) Ta có: ![]()
Trên khoảng ![]() ,
, ![]() ↔
↔ ![]() (thỏa mãn) hoặc
(thỏa mãn) hoặc ![]()

- Ta có:
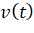 là vận tốc tức thời của con tàu ở thời điểm
là vận tốc tức thời của con tàu ở thời điểm  (s) kể từ khi đốt cháy các tên lửa hãm với
(s) kể từ khi đốt cháy các tên lửa hãm với  .
.
Khi đó: ![]() với
với ![]() .
.
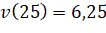 (km/s)
(km/s)- Tại thời điểm
 (s), lúc đó
(s), lúc đó 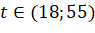 , căn cứ vào bảng biến thiên ở câu (b), ta thấy
, căn cứ vào bảng biến thiên ở câu (b), ta thấy 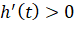 , tức là
, tức là  , vậy vận tốc tức thời của con tàu đang tăng trở lại.
, vậy vận tốc tức thời của con tàu đang tăng trở lại.
Bài 8: Xét phản ứng hóa học tạo ra chất ![]() từ hai chất
từ hai chất ![]() và
và ![]() :
:
![]()
Giả sử nồng độ của hai chất ![]() và
và ![]() bằng nhau
bằng nhau ![]() (mol/l). Khi đó, nồng độ của chất
(mol/l). Khi đó, nồng độ của chất ![]() theo thời gian
theo thời gian ![]() (
(![]() ) được cho bởi công thức:
) được cho bởi công thức: ![]() (mol/l), trong đó
(mol/l), trong đó ![]() là hằng số dương (Nguồn: Đỗ Đức Thái (Chủ biên) và các đồng tác giả, Giáo trình Phép tính vi tích phân hàm một biến, NXB Đại học Sư phạm, 2023).
là hằng số dương (Nguồn: Đỗ Đức Thái (Chủ biên) và các đồng tác giả, Giáo trình Phép tính vi tích phân hàm một biến, NXB Đại học Sư phạm, 2023).
- Tìm tốc độ phản ứng ở thời điểm
 .
. - Chứng minh nếu
 thì
thì  .
. - Nêu hiện tượng xảy ra với nồng độ các chất khi
 .
. - Nêu hiện tượng xảy ra với tốc độ phản ứng khi
 .
.
Giải nhanh:
- Ta có:
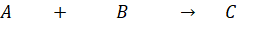
Ban đầu: ![]()
![]()
![]()
Sau thời gian ![]() :
: ![]()
![]()
![]()
Tốc độ ở thời điểm ![]() là
là ![]()
- Ta có:
 , tức là
, tức là  .
.


=> ![]()
Như vậy khi ![]() thì nồng độ các chất
thì nồng độ các chất ![]() ,
, ![]() và
và ![]() bằng nhau.
bằng nhau.
Như vậy khi ![]() , tốc độ phản ứng dần về 0, khi đó phản ứng kết thúc
, tốc độ phản ứng dần về 0, khi đó phản ứng kết thúc
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều



Bình luận