PHƯƠNG TRÌNH MẶT CẦU

I. ĐỊNH NGHĨA MẶT CẦU

Hoạt động 1 trang 81 sgk toán 12 tập 2 cd

Nếu quay đường tròn tâm I, bán kính R quanh đường kính AB một vòng (Hình 39) thì hình tạo thành được gọi là mặt cầu. Những điểm thuộc mặt cầu đó cách I một khoảng bằng bao nhiêu?

Giải nhanh:

Bằng bán kính R

Luyện tập-vận dụng 1 trang 81 sgk toán 12 tập 2 cd

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 2; 3) và mặt cầu tâm I đi qua điểm A(0; 4; 5). Tính bán kính R của mặt cầu đó.

Giải nhanh:

R =

II. PHƯƠNG TRÌNH MẶT CẦU

Luyện tập-vận dụng 2 trang 82 sgk toán 12 tập 2 cd

Tìm tâm và bán kính của mặt cầu có phương trình:

Giải nhanh:

Tâm I của mặt cầu: I(0;-5;1)

Bán kính mặt cầu:

Luyện tập-vận dụng 3 trang 82 sgk toán 12 tập 2 cd

Viết phương trình của mặt cầu, biết:

a) Tâm O bán kính R với O là gốc tọa độ

b) Đường kính AB với A(1;2;1), B(3;4;7)

Giải nhanh:

a) Mặt cầu có tâm O(0;0;0) và bán kính R có phương trình là:

b) Mặt cầu có đường kính AB với A(1;2;1), B(3;4;7)

Tâm I của mặt cầu là trung điểm đoạn thẳng AB: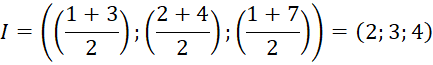

Bán kính R bằng độ dài đoạn AI:

Phương trình mặt cầu:

Luyện tập-vận dụng 4 trang 83 sgk toán 12 tập 2 cd

Chứng minh rằng phương trình là phương trình mặt cầu. Tìm tâm I và bán kính R của mặt cầu đó?

Giải nhanh:

Tâm của mặt cầu là I =(3,1,2)

Bán kính

III. MỘT SỐ ỨNG DỤNG CỦA PHƯƠNG TRÌNH MẶT CẦU TRONG THỰC TIỄN

Luyện tập-vận dụng 5 trang 85 sgk toán 12 tập 2 cd

Trong ví dụ 6 giả sử người đi biển di chuyển theo đường thẳng từ vị trí (21;35;50) đến vị trí D(5 121; 658; 0). Tìm vị trí cuối cùng trên đoạn thẳng ID sao cho người đi biển còn có thể nhìn thấy được ánh sáng từ ngọn hải đăng.

Giải nhanh:

Ta có phương trình mặt cầu mô tả ranh giới ngọn hải đăng:

Vị trí cuối cùng thấy ánh sáng cách tâm mặt cầu 1 đoạn bằng R:

Gọi M(x;y;z) là điểm cuối cùng thấy ánh sáng. Tọa độ M thỏa mãn:

M thuộc đoạn ID. Ta có vector chỉ phương của ID:

Phương trình tham số của đoạn ID:

Thay x,y,z vào phương trình mặt cầu: 

=>

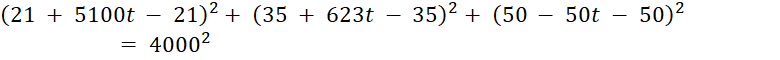
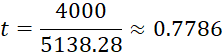
Tính tọa độ M:

BÀI TẬP

Bài 1 trang 85 sgk toán 12 tập 2 cd 

Tâm của mặt cầu có tọa độ là:

A. (-2; 3; 4)

B. (2; 3; -4)

C. (2; -3; -4)

D. (2; -3; 4)

Giải nhanh:

B. (2; 3; -4)

Bài 2 trang 85 sgk toán 12 tập 2 cd 

Bán kính của mặt cầu bằng:

A. 3

B. 9

C. 81

D.

Giải nhanh:

A. 3

Bài 3 trang 86 sgk toán 12 tập 2 cd 

Mặt cầu (S) tâm I(-5; -2; 3) bán kính 4 có phương trình là:

A.

B.

C.

D.

Giải nhanh:

B.

Bài 4 trang 86 sgk toán 12 tập 2 cd 

Cho mặt cầu có phương trình

a) Xác định tâm và bán kính của mặt cầu.

b) Mỗi điểm A(1; 1; 1), B(9; 4; 7), C(9; 9; 10) nằm trong, nằm ngoài hay nằm trên mặt cầu đó?

Giải nhanh:

a) Tâm I(1; -2; 7) và R = 10

b)  Điểm A(1; 1; 1) cách tâm I(1; -2; 7) một khoảng là nhỏ hơn bán kính R = 10. Do đó, điểm A nằm trong mặt cầu.

 Điểm B(9; 4; 7) cách tâm I(1; -2; 7) một khoảng là. Do đó, điểm B nằm trên mặt cầu.

Điểm C(9; 9; 10) cách tâm I(1; -2; 7) một khoảng là lớn hơn bán kính R = 10. Do đó, điểm C nằm ngoài mặt cầu.

Bài 5 trang 86 sgk toán 12 tập 2 cd 

Cho phương trình

Chứng minh rằng phương trình trên là phương trình của một mặt cầu. Xác định tâm và bán kính của mặt cầu đó.

Giải nhanh:

Ta có:

Vậy phương trình đã cho là phương trình mặt cầu

=> Mặt cầu có tâm I(2, 1, 5) và bán kính

Bài 7 trang 86 sgk toán 12 tập 2 cd 

Lập phương trình mặt cầu (S) trong mỗi trường hợp sau:

a) (S) có tâm I(3;-7;1) và bán kính R=2;

b) (S) có tâm I(-1;4;-5) và đi qua điểm M(3;1;2);

c) (S) có đường kính là đoạn thẳng CD với C(1;-3;-1)) và (D(-3:1;2)

Giải nhanh:

a)

b)

c)

Bài 7 trang 86 sgk toán 12 tập 2 cd 

Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian (Hình 42). Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau:

Trong cùng một thời điểm, toạ độ của một điểm M trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí M cần tìm toạ độ. Như vậy, điểm M là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.

Trong không gian với hệ toạ độ Oxyz, cho bốn vệ tinh A(3;-1; 6), B(1; 4; 8), C(7; 9; 6), D(7; 15; 18). Tìm toạ độ của điểm M trong không gian biết khoảng cách từ các vệ tinh đến điểm M lần lượt là MA = 6, MB = 7, MC = 12, MD = 24.

Giải nhanh:

Gọi (x, y, z) là toạ độ của điểm M.

Khoảng cách từ M đến các vệ tinh có thể được biểu diễn bởi các phương trình mặt cầu:

Ta có hệ phương trình:

Lấy (1)-(2):

Có:

Cộng lại, ta có:

Lấy (2)-(3):

Có:

Cộng lại, ta có:

Lấy (3)-(4)

Có:

Cộng lại, ta có:

Do đó, chúng ta có hệ 3 phương trình tuyến tính:

Giải hệ, ta có 

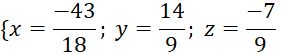
Vậy điểm