Dễ hiểu giải Toán 12 Cánh diều bài 4: Ứng dụng hình học của tích phân
Giải dễ hiểu bài 4: Ứng dụng hình học của tích phân. Trình bày rất dễ hiểu, nên tiếp thu Toán 12 Cánh diều dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
I. TÍNH DIỆN TÍCH HÌNH PHẲNG
1. Diện tích hình phẳng giới hạn bởi đồ thị hàm số (y=f(x)), trục hoành và hai đường thẳng (x=a, x=b)
Hoạt động 1 trang 29 sgk toán 12 tập 2 cd
Cho hàm số ![]() có đồ thị được minh họa ở Hình 11.
có đồ thị được minh họa ở Hình 11.

a) Quan sát Hình 11, hãy cho biết các hình phẳng ![]() lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào.
lần lượt được giới hạn bởi các đường thẳng và đồ thị hàm số nào.
b) Tính diện tích ![]() của các hình phẳng đó.
của các hình phẳng đó.
c) Gọi H là hợp của các hình phẳng ![]() .Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm
.Hình phẳng H được gọi là hình phẳng giới hạn bởi đồ thị hàm ![]() ,trục hoành và các đường thẳng x=0, x=3. Chứng tỏ rằng diện tích
,trục hoành và các đường thẳng x=0, x=3. Chứng tỏ rằng diện tích ![]() của hình phẳng H bằng:
của hình phẳng H bằng:

Giải nhanh:
a) Quan sát Hình 11, ta thấy:
Hình phẳng ![]() được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và các đường thẳng x=0, x=A
được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và các đường thẳng x=0, x=A
Hình phẳng ![]() được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=A, x=B
được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=A, x=B
Hình phẳng ![]() được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=B, x=3
được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=B, x=3
b) Diện tích H1 bằng diện tích của tam giác được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và đường thẳng x=A,x=0. Diện tích này có thể được tính bằng công thức: ![]()
Diện tích H2 bằng diện tích của tam giác được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và đường thẳng x=A, x=B. Diện tích này có thể được tính bằng công thức: ![]()
Diện tích H3 bằng diện tích của tam giác được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và đường thẳng x=B,x=3. Diện tích này có thể được tính bằng công thức: ![]()
c) Ta có:
![]()

Vậy diện tích ![]() của hình phẳng H bằng:
của hình phẳng H bằng:

Luyện tập-vận dụng 1 trang 30 sgk toán 12 tập 2 cd
Trong Hình 13, tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số ![]() trục Ox và hai đường thẳng
trục Ox và hai đường thẳng ![]() .
.

Giải nhanh:
Diện tích hình phẳng giới hạn bởi đồ thị của hàm số ![]() trục Ox và hai đường thẳng
trục Ox và hai đường thẳng ![]() là:
là:

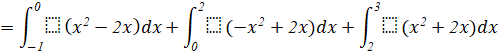

![]()
![]()
![]()
2. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số (y=f(x) y=g(x)) và hai đường thẳng (x=a x=b)
Hoạt động 2 trang 31 sgk toán 12 tập 2 cd
Cho các hàm số ![]()
Gọi ![]() là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x=1 x=2 và đồ thị hàm số
là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x=1 x=2 và đồ thị hàm số ![]()
Gọi ![]() là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x=1 x=2 và đồ thị hàm số y=x
là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x=1 x=2 và đồ thị hàm số y=x
Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số ![]() và hai đường thẳng x=1 x=2 (Hình 14).
và hai đường thẳng x=1 x=2 (Hình 14).
a) Biểu diễn S theo ![]()
b) So sánh S và ![]()
Giải nhanh:
a) ![]()
b) Ta có:
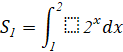


Luyện tập-vận dụng 2 trang 32 sgk toán 12 tập 2 cd
Tính diện tích hình phẳng được giới hạn bởi các đồ thị hàm số ![]() và 2 đường thẳng x=-2, x=2
và 2 đường thẳng x=-2, x=2
Giải nhanh:
Với ![]()
![]()
Vậy diện tích hình phẳng đó là:

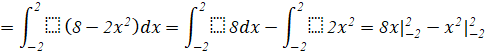
![]()
II. TÍNH THỂ TÍCH HÌNH KHỐI
1. Thể tích của vật thể:
Hoạt động 3 trang 35 sgk toán 12 tập 2 cd
Cắt khối lập phương có cạnh bằng 1 bởi một mặt phẳng tùy ý vuông góc với trục Ox tại x, với ![]() ta nhận được một hình phẳng với diện tích là S(x) (Hình 17).
ta nhận được một hình phẳng với diện tích là S(x) (Hình 17).
a) Tính S(x)
b) So sánh thể tích khối lập phương đó với ![]()
Giải nhanh:
a) Khi cắt khối lập phương bởi một mặt phẳng vuông góc với trục Ox tại x, ta thu được một hình phẳng có chiều dài là 1 và chiều rộng là 1. Do đó, diện tích của hình phẳng này là:
![]()
b) Thể tích khối lập phương có cạnh bằng 1 là:
![]()
Tích phân của S(x) trên đoạn [0;1] :
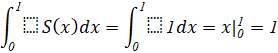
Luyện tập-vận dụng 3 trang 35 sgk toán 12 tập 2 cd
Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x = 1 và x = 2. Một mặt phẳng tùy ý vuông góc với Ox tại x (1 ≤ x ≤ 2) cắt vật thể đó theo hình phẳng có diện tích là S(x) = 2x. Tính thể tích V của phần vật thể được giới hạn bởi hai mặt phẳng trên.
Giải nhanh:
Thể tích V của phần vật thể được giới hạn bởi 2 mặt phẳng đã cho là:

Luyện tập-vận dụng 4 trang 37 sgk toán 12 tập 2 cd
Cho khối chóp cụt đều tạo bởi khối chóp đỉnh S, diện tích hai đáy lần lượt là B, B' và chiều cao h. Chọn trục Ox chứa đường cao của khối chóp và gốc O trùng với đỉnh S (Hình 21). Hai mặt phẳng đáy của khối chóp cụt đều lần lượt cắt Ox tại I và I'.
Đặt OI = b, OI' = a (a < b). Một mặt phẳng P vuông góc với trục Ox tại x (a≤x≤b), cắt khối chóp cụt đều theo hình phẳng có diện tích S(x). Người ta chứng minh rằng ![]() Tính thể tích khối chóp cụt đều đó.
Tính thể tích khối chóp cụt đều đó.
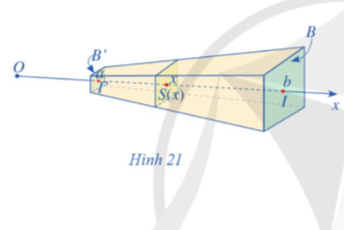
Giải nhanh:
Thể tích khối chóp đó là:

2. Thể tích khối tròn xoay
Hoạt động 4 trang 38 sgk toán 12 tập 2 cd
Xét nửa hình tròn tâm O, bán kính r(Hình 24). Nửa hình tròn đó là hình phẳng giới hạn bởi trục Ox và đồ thị hàm số y=f(x)
a) Tìm hàm số y = f(x)
b) Quay nửa hình tròn đó quanh trục hoành, ta nhận được hình cầu tâm O bán kính r. Xét điểm M(x; f(x)) (-r ≤ x ≤ r) nằm trên nửa đường tròn tâm O bán kính r. Gọi H(x ; 0) là hình chiếu của điểm M trên trục Ox. Khi quay nửa hình tròn quanh trục hoành, đoạn thẳng HM tạo nên một hình tròn tâm H bán kính f(x).
Tính diện tích S(x) của hình tròn đó theo f(x).
Từ đó, sử dụng công thức tính thể tích vật thể, hãy tính thể tích V của hình cầu tâm Q bán kính r.
Giải nhanh:
a)
Để tìm hàm số y = f(x), ta cần xác định phương trình của nửa hình tròn.
Ta có hình tròn tâm O, bán kính r có phương trình là:
![]()
Do đồ thị của nửa hình tròn nằm ở nửa trên trục Ox, tức là phần dương của đồ thị. Vậy nửa hình tròn giới hạn bởi trục Ox và đồ thị hàm số y = f(x) có phương trình là:
![]()
b)
Diện tích S(x) của hình tròn tâm H bán kính f(x) là:
![]()
Thể tích V của hình cầu tâm O tính theo công thức tính thể tích của vật thể là:



Luyện tập-vận dụng 5 trang 39 sgk toán 12 tập 2 cd
Cho hình phẳng giới hạn bởi đồ thị hàm số ![]() trục hoành và hai đường thẳng
trục hoành và hai đường thẳng ![]() Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.
Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.
Giải nhanh:
Thể tích khối tròn xoay tạo ra từ hình phẳng giới hạn bởi đồ thị hàm số ![]() trục hoành và hai đường thẳng
trục hoành và hai đường thẳng ![]() khi quay quanh trục Ox là:
khi quay quanh trục Ox là:
![]()
![]()
GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA
Bài 1 trang 40 toán 12 tập 2 cd
Hình thang cong ABCD ở Hình 28 có diện tích bằng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()

Giải nhanh:
B. ![]()
Bài 2 trang 40 toán 12 tập 2 cd
Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số ![]() trục hoành và 2 đường thẳng x=0, x=2 quay quanh trục Ox là:
trục hoành và 2 đường thẳng x=0, x=2 quay quanh trục Ox là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giải nhanh:
B. ![]()
Bài 3 trang 41 toán 12 tập 2 cd
Cho đồ thị hàm số ![]() và hình phẳng được tô màu như hình 29.
và hình phẳng được tô màu như hình 29.
a) Hình phẳng đó được giới hạn bởi những đường nào?
b) Tính diện tích hình phẳng đó.

Giải nhanh:
a) Dựa vào Hình 29, ta thấy hình phẳng đã cho được giới hạn bởi các đường ![]() và trục hoành.
và trục hoành.
b) Diện tích của hình phẳng đã cho là:

Bài 4 trang 41 toán 12 tập 2 cd
Cho đồ thị các hàm số ![]() và hình phẳng được tô màu như hình 30.
và hình phẳng được tô màu như hình 30.
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó

Giải nhanh:
a) Nhìn vào hình 29, ta thấy hình phẳng đã cho được giới hạn bởi trục tung và các đường ![]()
b) Ta thấy trong đoạn [0;2], ![]()
Diện tích hình phẳng đã cho là:

![]()
Bài 5 trang 41 toán 12 tập 2 cd
Cho đồ thị hàm số ![]() và khối tròn xoay như hình 31.
và khối tròn xoay như hình 31.
a) Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục Ox ta được khối tròn xoay như hình 31?
b) Tính thể tích khối tròn xoay đó.
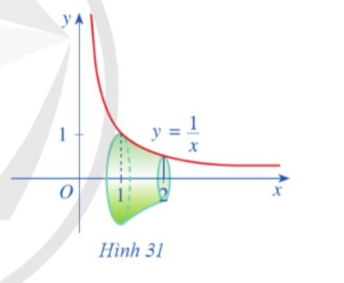
Giải nhanh:
a) Để được khối tròn xoay như hình 31, hình phẳng cần được giới hạn bởi trục hoành Ox, các đường ![]()
b) Thể tích khối tròn xoay là:
![]()
Bài 6 trang 41 toán 12 tập 2 cd
Cho đồ thị hàm số như hình 32.
a) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(t), trục Ot và 2 đường thẳng t=0, t=2.
b) Hỏi ![]() biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32?
biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường nào trong Hình 32?

Giải nhanh:
a)

Kẻ đường x=2 cắt đồ thị f(t) tại điểm B.Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(t), trục Ot và 2 đường thẳng t=0, t=2 là phần diện tích hình thang OABC như trên hình vẽ:
![]()
b) ![]() biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường
biểu thị cho phần diện tích của hình phẳng giới hạn bởi các đường ![]()
Bài 7 trang 42 toán 12 tập 2 cd
Người ta dự định lắp kính cho cửa của một mái vòm có dạng hình parabol. Hãy tính diện tích mặt kính cần lắp vào, biết rằng vòm cửa cao 21 m và rộng 70 m (Hình 33).

Giải nhanh:
Mái vòm có dạng hình parabol, tức là có dạng phương trình ![]()
Theo đề bài, vòm cửa cao 21 m và rộng 70 m. Chọn trục tung đi qua đỉnh parabol. Vậy đỉnh parabol có hoành độ y= 21 và parabol cắt trục hoành tại điểm x=-35 và x=35. Thay x=35,y=21 vào phương trình parabol, ta được:
![]()
![]()
Vậy mái vòm parabol có phương trình là:
![]()
Diện tích mặt kính cửa mái vòm là diện tích hình phẳng giới hạn bởi trục Ox, đường thẳng ![]() và đường
và đường ![]() :
:

Vậy diện tích mặt kính cửa mái vòm cần lắp vào là 490m2
Bài 8 trang 42 toán 12 tập 2 cd
Hình 34 minh họa mặt cắt đứng của một con kênh đặt trong hệ trục tọa độ Oxy. Đáy của con kênh là một đường cong được cho bởi phương trình:
![]()
Hãy tính diện tích hình phẳng tô màu xanh trong hình 34, biết mỗi đơn vị trên mỗi trục tọa độ là mét.

Giải nhanh:
Theo hình 34, hình phẳng được tô màu xanh được giới hạn bởi trục Ox, các đường ![]()
Diện tích hình phẳng đã cho là:



![]()
Bài 9 trang 42 toán 12 tập 2 cd
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox.
Giả sử ![]()
Gọi N là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích N theo ![]() và
và ![]()
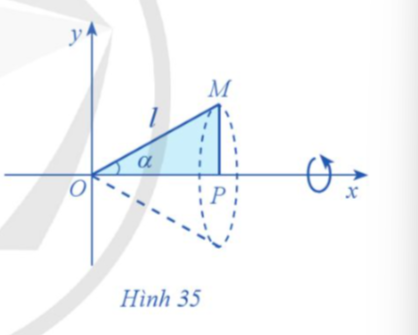
Giải nhanh:
Để tính thể tích của khối tròn xoay N, ta cần tính diện tích mặt đáy (hình tròn) và tích phân diện tích mặt đáy theo chiều cao (độ dài đoạn OM).
Diện tích mặt đáy hình tròn là:
![]()
Ta có:
P nằm trên trục tọa độ:
![]() Điểm P có tọa độ
Điểm P có tọa độ ![]()
PM vuông góc với trục Ox:
![]() Điểm M có tọa độ
Điểm M có tọa độ ![]()
O có tọa độ (0;0)
Hệ số góc của đường thẳng OM:
![]()
Vì OM qua gốc tọa độ, phương trình đường thẳng OM có dạng:
![]()
Thể tích khối tròn xoay N được giới hạn bởi đường ![]() :
:
![]()
![]()
Bài 10 trang 42 toán 12 tập 2 cd
Sau khi đo kích thước của thùng rượu vang (Hình 36), bạn Quân xác định thùng rượu vang có dạng hình tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số
![]()
trục Ox và hai đường thẳng x=−35, x=35 quay quanh trục Ox. Tính thể tích thùng rượu vang đó, biết đơn vị trên mỗi trục toạ độ là centimét.

Giải nhanh:
Thể tích thùng rượu vang là:





![]()
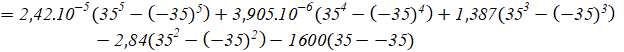
![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận