Soạn giáo án điện tử toán 11 Cánh diều Chương 8 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối

Nội dung giáo án

CHÀO MỪNG CẢ LỚP
ĐẾN VỚI TIẾT HỌC
 HÔM  NAY!

KHỞI ĐỘNG

Ở lớp 7, ta đã làm quen với hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác, tức là những hình lăng trụ đứng có đáy là tam giác hoặc tứ giác

Hình lăng trụ đứng với đáy là đa giác, đặc biệt là đa giác đều, có tính chất gì?

BÀI 6. HÌNH LĂNG TRỤ ĐỨNG.

HÌNH CHÓP ĐỀU.

HÌNH LĂNG TRỤ ĐỀU

NỘI DUNG BÀI HỌC

Hình lăng trụ đứng. Hình lăng trụ đều

Hình chóp đều. Hình chóp cụt đều

Thể tích của một số hình khối

I

Hình lăng trụ đứng. Hình lăng trụ đều

HĐ1: Cho hình lăng trụ tam giác có các mặt bên là hình chữ nhật ở Hình 80a, 80b. Hãy cho biết mỗi cạnh bên của hình lăng trụ đó có vuông góc với các mặt đáy hay không.

Giải:

Ta có: AA′⊥AC (A′ACC′ là hình chữ nhật)

           AA′⊥AB (A′ABB′ là hình chữ nhật)

⇒AA^′⊥(ABC).

Chứng minh tương tự, ta cũng có:

BB^′⊥(ABC);CC^′⊥(ABC).

Định nghĩa

Hình lăng trụ có cạnh bên vuông góc với mặt đáy được gọi là hình lăng trụ đứng.

Hình lăng trụ đứng có đáy là đa giác đều gọi là hình lăng trụ đều.

Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.

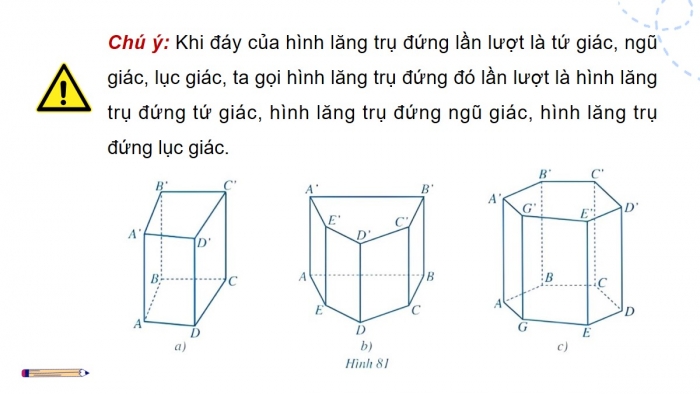
Chú ý: Khi đáy của hình lăng trụ đứng lần lượt là tứ giác, ngũ giác, lục giác, ta gọi hình lăng trụ đứng đó lần lượt là hình lăng trụ đứng tứ giác, hình lăng trụ đứng ngũ giác, hình lăng trụ đứng lục giác.

Nhận xét:

Mỗi mặt bên của hình lăng trụ đứng là hình chữ nhật, mặt phẳng chứa nó vuông góc với mặt đáy.

Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Hình hộp chữ nhật có 6 mặt là hình chữ nhật.

Nếu mỗi mặt của hình hộp là hình chữ nhật thì hình hộp đó là hình hộp chữ nhật.

Độ dài các đường chéo của hình hộp chữ nhật là bằng nhau.

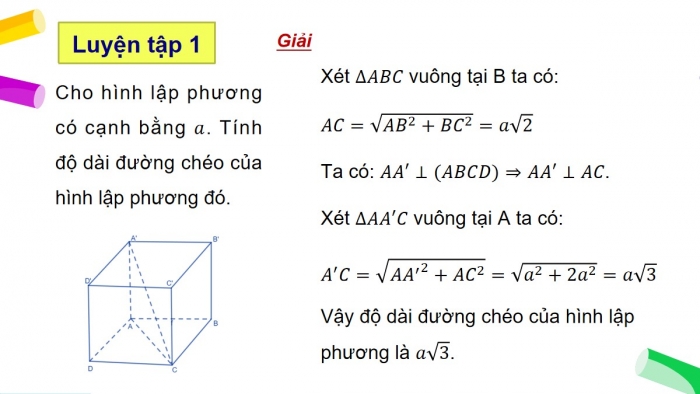
Hình lập phương là hình chữ nhật có tất cả các mặt là hình vuông.

Hình lập phương là hình lăng trụ tứ giác đều có cạnh bên bằng cạnh đáy.

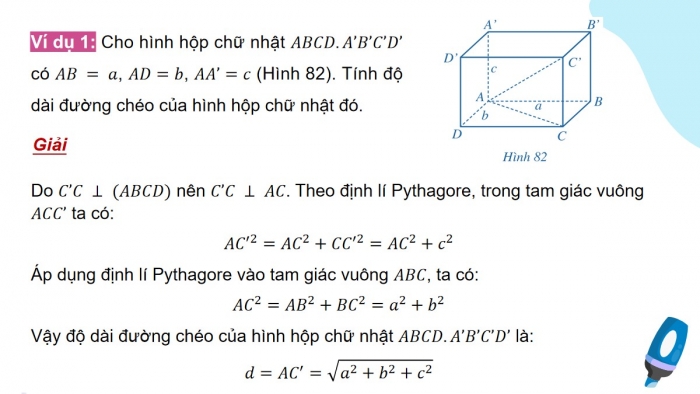
Ví dụ 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD=b, AA’=c (Hình 82). Tính độ dài đường chéo của hình hộp chữ nhật đó.

Giải

Do C’C ⊥ (ABCD) nên C’C ⊥ AC. Theo định lí Pythagore, trong tam giác vuông ACC’ ta có:

AC^′2=AC^2+CC^′2=AC^2+c^2

Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

AC^2=AB^2+BC^2=a^2+b^2

Vậy độ dài đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’ là:

d=AC^′=√a^2+b^2+c^2