Soạn giáo án điện tử toán 11 Cánh diều Bài 1: Đường thẳng và mặt phẳng trong không gian

Nội dung giáo án

NHIỆT LIỆT CHÀO ĐÓN CẢ LỚP ĐẾN VỚI BÀI HỌC MỚI!

KHỞI ĐỘNG

Quan sát hình ảnh sau:

Em hãy kể thêm một số hình ảnh của Hình học không gian trong thực tế.

Khối rubic

Bánh ít

Quả bóng

Bánh chưng

CHƯƠNG IV. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG

BÀI 1: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

NỘI DUNG BÀI HỌC

Khái niệm mở đầu

Các tính chất thừa nhận của hình học không gian

Một số cách xác định mặt phẳng

Hình chóp và hình tứ diện

1. KHÁI NIỆM MỞ ĐẦU
2. Mặt phẳng

• Điểm và đường thẳng là đối tượng cơ bản của hình học phẳng. Từ điểm, đường thẳng và quan hệ cơ bản giữa chúng → xây dựng nên hình học phẳng.
• Với hình học không gian có ba đối tượng cơ bản: điểm, đường thẳng, mặt phẳng.

HĐ1

Sân vận động Old Trafford (Hình 2) ở thành phố Manchester, có biệt danh là “Nhà hát của những giấc mơ”, với sức chứa 75 635 người, là sân vận động lớn thứ hai ở Vương quốc Anh.

Quan sát Hình 2 và cho biết mặt sân vận động thường được làm phẳng hay cong.

> Mặt sân vận động được làm phẳng

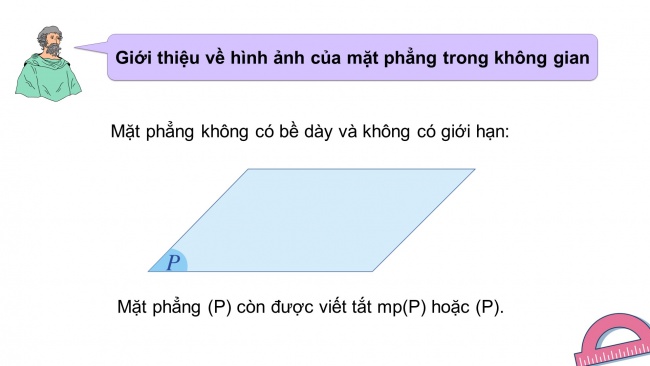
Giới thiệu về hình ảnh của mặt phẳng trong không gian

Mặt phẳng không có bề dày và không có giới hạn:

Mặt phẳng (P) còn được viết tắt mp(P) hoặc (P).

Luyện tập 1

Nêu ví dụ trong thực tiễn minh họa hình ảnh của một phần mặt phẳng.

Bảng treo tường

Mặt bàn

Tấm gương phẳng

Nền nhà

Bức tường

2. Điểm thuộc mặt phẳng

HĐ2

Quan sát Hình 1, nếu coi mặt sân Napoléon là một phần của mặt phẳng (P) thì đỉnh của kim tự tháp có thuộc mặt phẳng (P) hay không?

Đỉnh của kim tự tháp không thuộc mặt phẳng (P).

Nhận xét:

Với mỗi điểm A và mp (P) chỉ xảy ra một trong hai khả năng:

• Điểm A thuộc mặt phằng (P), kí hiệu A ∈ (P). Ta còn nói A nằm trong (hay nằm trên) mặt phẳng (P) hay mặt phẳng (P) đi qua điểm A.
• Điểm A không thuộc mặt phẳng (P), A ∉(P). Ta còn nói A nằm ngoài (P).

3. Hình biểu diễn của một hình trong không gian
4. a) Khái niệm

Hình ảnh kim tự tháp có hình biểu diễn như sau:

Khái niệm:

Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian gọi là hình biểu diễn của hình không gian đó.

1. b) Quy tắc vẽ hình biểu diễn của hình trong không gian

• Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng được biểu diễn bởi đoạnt hẳng.
• Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau).
• Hình biểu diển giữ nguyên tính liên thuộc giữa điểm với đường thẳng hoặc với đoạn thẳng.
• Những đường nhìn thấy được vẽ bằng nét liền, những đường không nhìn thấy được vẽ bằng nét đứt.

Ví dụ hình biểu diễn một số hình thường gặp:

Ví dụ 1

Dựa trên Hình 7, vẽ hình biểu diễn của hộp phấn

Giải

Hình biểu diễn của hộp phấn có thể vẽ như Hình 8:

Luyện tập 2

Vẽ hình biểu diễn của mặt phẳng (P) và đường thẳng a xuyên qua nó.

Chú ý: Phần không nhìn thấy được của đường thẳng a vẽ bằng nét đứt.

1. CÁC TÍNH CHẤT THỪA NHẬN CỦA HÌNH HỌC KHÔNG GIAN

Thảo luận nhóm đôi, thực hiện HĐ3, HĐ4, HĐ5

HĐ3

Quan sát Hình 9 và cho biết ta cần bao nhiêu điểm đỡ để giữ cố định được xà ngang đó.

Giải

Cần có 2 điểm đỡ để giữ cố định được xà ngang.

Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước

HĐ4

“Kiềng ba chân” là vận dụng bằng sắt, có hình vòng cung được gắn ba chân, dùng để đặt nồi lên khi nấu bếp. Bếp củi và kiềng ba chân là hình ảnh hết sức quen thuộc với gia đình ở Việt Nam. Vì sao kiềng ba chân khi đặt trên mặt đất không bị cập kênh?

Giải:

Vì ba điểm chân kiềng sẽ cùng nằm trên mặt phẳng là nền đất.

Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

Ví dụ

Mặt phẳng qua ba điểm A, B, C không thẳng hàng được kí hiệu là mp(ABC) hoặc (ABC).

Lấy hai điểm trên mặt phẳng bảng, đặt thước qua hai điểm đó và vẽ 1 đường thẳng. Khi đó mọi điểm của đường thẳng có thuộc mặt phẳng bảng không?

Tính chất 3

Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Nhận xét:

Nếu đường thẳng d đi qua hai điểm phân biệt A, B của mặt phẳng (P) thì đường thẳng d nằm trong mặt phẳng (P) hoặc (P) chứa d, hoặc (P) đi qua d, thường được kí hiệu là d ⊂ (P) hoặc (P) ⊂ d.

Áp dụng tính chất để giải thích Ví dụ 2.

Ví dụ 2