Soạn giáo án điện tử toán 11 Cánh diều Bài 1: Dãy số
Giáo án powerpoint toán 11 Cánh diều mới. Giáo án soạn theo tiêu chí hiện đại, đẹp mắt với nhiều hình ảnh, nội dung, hoạt động phong phú, sáng tạo. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu. Tin rằng, bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng với thầy cô.
Xem hình ảnh về giáo án
Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
THÔNG TIN GIÁO ÁN
- Giáo án word: Trình bày mạch lạc, chi tiết, rõ ràng
- Giáo án điện tử: Sinh động, hiện đại, đẹp mắt để tạo hứng thú học cho học sinh
- Giáo án word và PPT đồng bộ, thống nhất với nhau
Khi đặt:
- Giáo án word: Nhận đủ cả năm
- Giáo án điện tử: Nhận đủ cả năm
PHÍ GIÁO ÁN:
- Giáo án word: 350k/học kì - 400k/cả năm
- Giáo án Powerpoint: 450k/học kì - 500k/cả năm
- Trọn bộ word + PPT: 600k/học kì - 700k/cả năm
=> Khi đặt, nhận giáo án ngay và luôn
CÁCH ĐẶT:
- Bước 1: gửi phí vào tk: 10711017 - Chu Văn Trí - Ngân hàng ACB (QR)
- Bước 2: Nhắn tin tới Zalo Fidutech - nhấn vào đây để thông báo và nhận giáo án
Nội dung giáo án
CHÀO MỪNG CẢ LỚP ĐẾN VỚI BÀI HỌC MỚI!
KHỞI ĐỘNG
Một số loài hoa có số lượng cánh hoa luôn là một số cố định. Số cánh hoa trong các bông hoa thường xuất hiện nhiều theo những con số 1, 1, 2, 3, 5, 8, 13, 21,...
Ta có thể viết số cánh hoa của các bông hoa ở các hình trên lần lượt như sau: vị trí thứ nhất viết số 1, vị trí thứ hai viết số 1, vị trí thứ ba viết số 2,..., vị trí thứ tám viết số 21.
Các số 1,1,2,3,5,8,13,21 được viết theo quy tắc trên gợi nên khái niệm nào trong toán học
CHƯƠNG II. DÃY SỐ. CẤP SỐ CỘNG.
CẤP SỐ NHÂN
BÀI 1: DÃY SỐ
NỘI DUNG BÀI HỌC
Khái niệm
Cách cho một dãy số
Dãy số tăng, dãy số giảm
Dãy số bị chặn
- KHÁI NIỆM
Một vật chuyển động đều với vận tốc 20 m/s. Hãy viết các số chỉ quãng đường (đơn vị: mét) vật chuyển độn được lần lượt trong thời gian 1 giây, 2 giây, 3 giây, 4 giây, 5 giây
Giải:
Quãng đường vật chuyển động được trong thời gian 1 giây là:
20 . 1 = 20 (m).
Quãng đường vật chuyển động được trong thời gian 2 giây là:
20 . 2 = 40 (m).
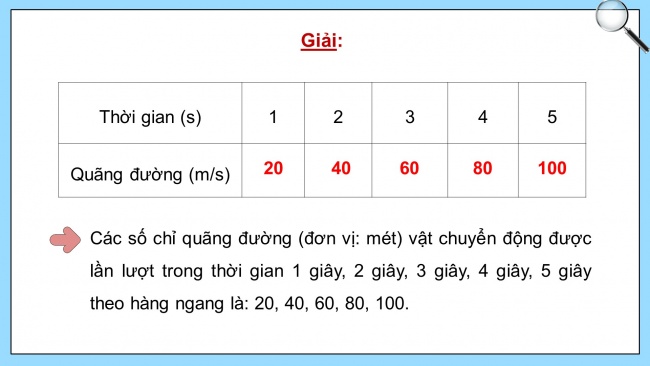
Thời gian (s) | 1 | 2 | 3 | 4 | 5 |
Quãng đường (m/s) |
Các số chỉ quãng đường (đơn vị: mét) vật chuyển động được lần lượt trong thời gian 1 giây, 2 giây, 3 giây, 4 giây, 5 giây theo hàng ngang là: 20, 40, 60, 80, 100.
KHÁI NIỆM
- Mỗi hàm số được gọi là một dãy số hữu hạn.
Do mỗi số nguyên dương k tương ứng với đúng một số nên ta có thể viết dãy số đó dưới dạng khai triển: .
- Số được gọi là số hạng đầu, số được gọi là số hạng cuối của dãy số đó.
Ví dụ 1 (SGK - tr.44)
Hàm số xác định trên tập hợp là một dãy số hữu hạn. Tìm số hạng đầu, số hạng cuối và viết dã số trên dưới dạng khai triển
Giải
Số hạng đầu, số hạng cuối của dãy số lần lượt là:
Dạng khai triển của dãy số đó là: 2, 4, 6, 8, 10.
Luyện tập 1
Hàm số xác định trên tập hợp là một dãy số hữu hạn. Tìm số cuối về viết dãy số trên dưới dạng khai triển
Giải
Số hạng đầu của khai triển là:
Số hạng cuối của khai triển là: .
Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125.
HĐ2
Cho hàm số . Hãy viết các số , , … , … theo hàng ngang
Giải:
Ta có:
Hãy cho biết dãy số trên là dãy vô hạn hay dãy hữu hạn?
Vô hạn
KHÁI NIỆM
+ Mỗi hàm số: được gọi là một dãy số vô hạn.
Do mỗi số nguyên dương n tương ứng với đúng một số nên ta có thể viết dãy số đó dưới dạng khai triển:
+ Dãy số đó còn được viết tắt là .
+ Số gọi là số hạng thứ nhất (hay số hạng đầu), số gọi là số hạng thứ hai,…, số gọi là số hạng thứ và là số hạng tổng quát của dãy số đó.
Chú ý:
Dãy số không đổi là dãy số có tất cả các số hạng đều bằng nhau
Thảo luận nhóm đôi, hoàn thành Ví dụ2
Cho là dãy các số tự nhiên lẻ viết theo thứ tự tăng dần và
- a) Viết năm số hạng đầu của dãy số
- b) Dựa đoán số hạng tổng quát và viết dạng khai triển của dãy số
Giải
- a) Năm số hạng đầu của dãy số là:
- b) Số hạng tổng quát của dãy số được dự đoán là với
Dạng khai triển của dãy số là:
Luyện tập 2
Cho dãy số với
- a) Viết năm số hạng đầu của dãy số
- b) Viết dạng khai triển của dãy số
Giải
- a) Năm số hạng đầu của dãy số là:
Số hạng tổng quát của dãy số là với .
- b) Dạng khai triển của dãy số:
- CÁCH CHO MỘT DÃY SỐ
Xét mỗi dãy số sau:
- Dãy số: (1)
- Dãy số được xác định như sau: Với mỗi số tự nhiên , là số thập phân hữu hạn có phần số nguyên là 1 và phần thập phân là chữ số thập phân đầu tiên đứng sau dấu “,” của số Cụ thể là: (2)
- Dãy số với (3)
- Dãy số được xác định như sau: và với mọi (4)
- a) Hãy nêu cách xác định mỗi số hạng của các dãy số (1), (2), (3), (4).
- b) Từ đó hãy cho biết dãy số có thể chho bằng những cách nào.
Giải:
- a) Cách xác định mỗi số hạng của các dãy số đã cho là:
- Dãy số (1) được xác định bằng cách liệt kê.
- Dãy số (2) được xác định bằng cách diễn đạt bằng lời cách xác định mỗi số hạng của dãy số đó.
- Dãy số (3) được xác định bằng cách cho công thức của số hạng tổng quát của dãy số đó.
- Dãy số (4) được xác định bằng cách cho bằng phương pháp quy hồi.
- b) Từ ý a) ta có thể thấy dãy số có thể cho bằng 4 phương pháp: liệt kê, diễn đạt bằng lời các xác định mỗi số hạng của dãy số đó, cho công thức của số hạng tổng quát của dãy số đó, cho bằng phương pháp quy hồi.
KẾT LUẬN