Soạn giáo án điện tử toán 11 Cánh diều: Bài tập cuối chương 7

Nội dung giáo án

CHÀO MỪNG CẢ LỚP

ĐẾN VỚI TIẾT HỌC HÔM NAY!

TRÒ CHƠI TRẮC NGHIỆM

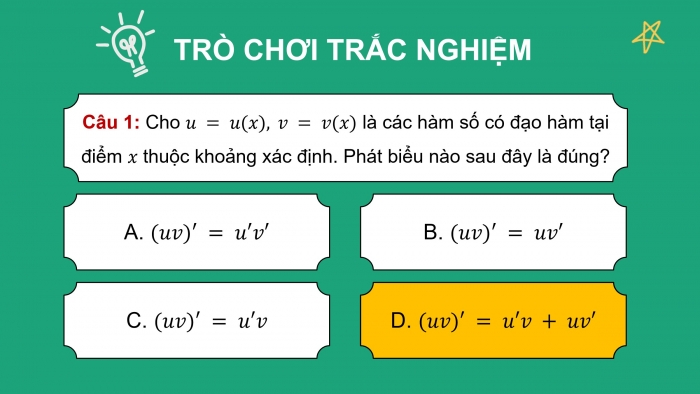
Câu 1: Cho u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

1. (uv)′ = u′v′
2. (uv)′ = uv′
3. (uv)′ = u′v
4. (uv)′ = u′v + uv′

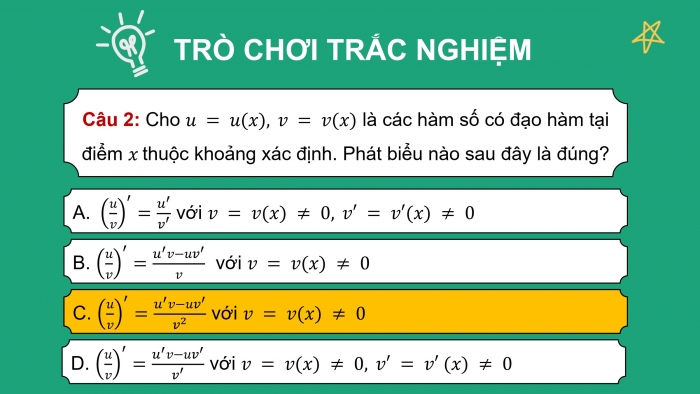
Câu 2: Cho u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

1.  (u/v)^′=u^′/v^′ với v = v(x) ≠ 0, v′ = v′(x) ≠ 0
2. (u/v)^′=u^′v−uv^′/v  với v = v(x) ≠ 0
3. (u/v)^′=u^′v−uv^′/v^2 với v = v(x) ≠ 0
4. (u/v)^′=u^′v−uv^′/v^′ với v = v(x) ≠ 0, v′ = v′ (x) ≠ 0

BÀI TẬP CUỐI CHƯƠNG VII

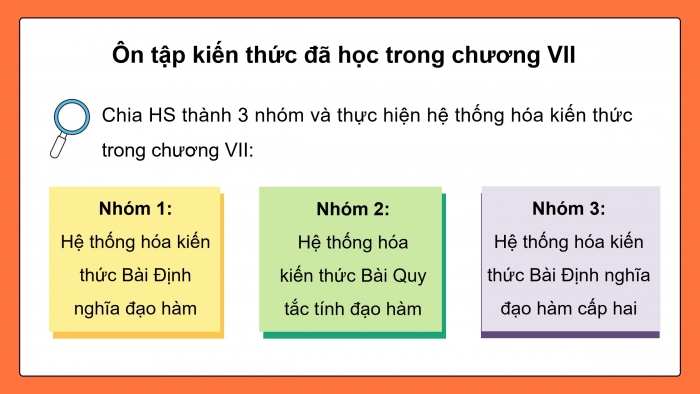
Ôn tập kiến thức đã học trong chương VII

Chia HS thành 3 nhóm và thực hiện hệ thống hóa kiến thức trong chương VII:

Nhóm 1:

Hệ thống hóa kiến thức Bài Định nghĩa đạo hàm

Nhóm 2:

Hệ thống hóa kiến thức Bài Quy tắc tính đạo hàm

Nhóm 3:

Hệ thống hóa kiến thức Bài Định nghĩa đạo hàm cấp hai

Định nghĩa đạo hàm và ý nghĩa hình học của đạo hàm.

Định nghĩa đạo hàm

Cho hàm số y = f(x) xác định trên khoảng (a;b) và điểm x_0∈(a;b).

Nếu tồn tại giới hạn lim┬x_1→x_0f(x_1)−f(x_0)/x_1−x_0 thì giới hạn đó được gọi là đạo hàm của hàm số y = f(x) tại x_0 và được kí hiệu f^′(x_0) hoặc y^′(x_0).

Cách tính đạo hàm bằng định nghĩa

Cho hàm số y = f(x) xác định trên khoảng (a;b) và điểm x_0∈(a;b).

Để tính đạo hàm f^′(x_0) của hàm số y = f(x) tại x_0, ta lần lượt thực hiện các bước sau:

Bước 1: Xét ∆x là số gia của biến số tại điểm x_0. Tính ∆y =f(x_0+∆x)−f(x_0).

Bước 2: Rút gọn tỉ số ∆y/∆x.

Bước 3: Tính lim┬∆x→0∆y/∆x.

Kết luận: Nếu lim┬∆x→0∆y/∆x =a thì f^′(x_0)=a.

Phương trình tiếp tuyến

Đạo hàm của hàm số y=f(x) tại điểm x_0 là hệ số góc của tiếp tuyến của đồ thị hàm số đó tại điểm M_0(x_0;f(x_0)).

Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm M_0(x_0;f(x_0)) là y = f^′(x_0)(x−x_0)+f(x_0).