Soạn giáo án điện tử toán 11 Cánh diều Chương 3 Bài 3: Hàm số liên tục

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Cầu Sông Hàn là một trong những cây cầu bắc qua sông Hàn ở Đà Nẵng. Đây là cây cầu quay  đầu tiên do kĩ sư, công nhân Việt Nam tự thiết kế và thi công. Khi cầu không quay (Hình 10a), mặt cầu liền mạch nên các phương tiện đường bộ có thể đi lại giữa hai đầu cầu. Khi cầu quay (Hình 10b) để các tàu, thuyền có thể đi qua thì mặt cầu không còn liền mạch nữa, các phương tiện đường bộ không thể đi qua giữa hai đầu cầu.

Kiến thức gì trong toán học thể hiện chuyển động có đường đi là đường liền mạch?

CHƯƠNG III. GIỚI HẠN. HÀM SỐ LIÊN TỤC

BÀI 3: HÀM SỐ LIÊN TỤC

NỘI DUNG BÀI HỌC

01 KHÁI NIỆM

1. Hàm số liên tục tại một điểm

HĐ 1: Quan sát đồ thị hàm số  ở Hình 11.

1. a) Tính 
2. b) So sánh với

KHÁI NIỆM Cho hàm số  xác định trên khoảng  và . Hàm số  được gọi là liên tục tại điểm  nếu .

Nhận xét: Hàm số  không liên tục tại  được gọi là gián đoạn tại .

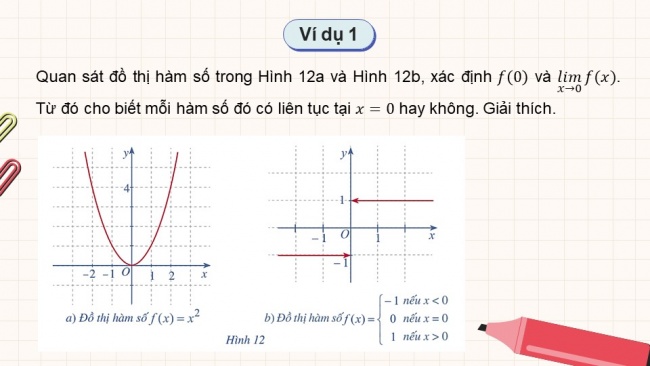
Ví dụ 1

Quan sát đồ thị hàm số trong Hình 12a và Hình 12b, xác định  và . Từ đó cho biết mỗi hàm số đó có liên tục tại hay không. Giải thích.

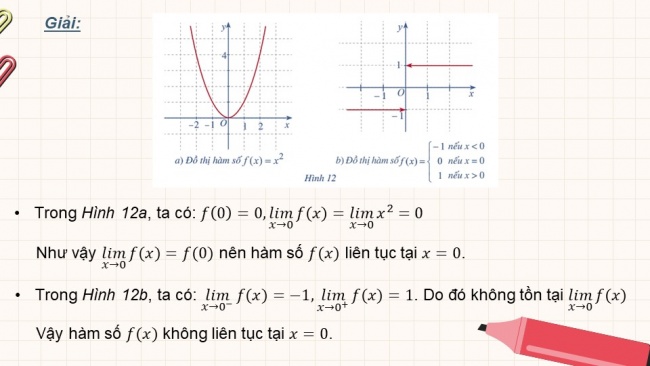
• Trong Hình 12a, ta có:
• Như vậy nên hàm số  liên tục tại .
• Trong Hình 12b, ta có: . Do đó không tồn tại
• Vậy hàm số không liên tục tại .

LUYỆN TẬP 1

Xét tính liên tục của hàm số  tại

Ta có:  và

Suy ra

Vì vậy hàm số liên tục tại .

2. Hàm số liên tục trên một khoảng hoặc một đoạn

Cho hàm số với .

1. a) Giả sử . Hàm số có liên tục tại điểm hay không?
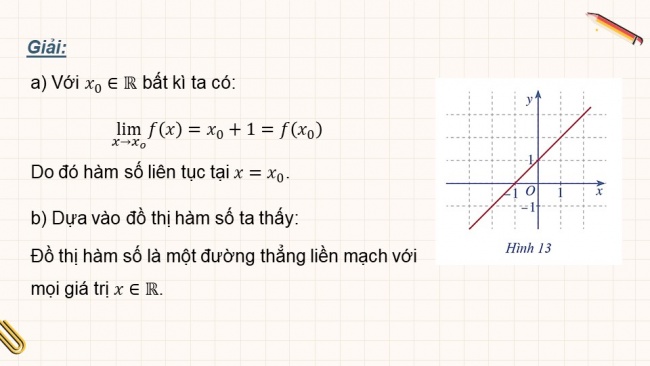
2. b) Quan sát đồ thị hàm số với (Hình 13), nêu nhận xét về đặc điểm của đồ thị hàm số đó.
3. a) Với bất kì ta có:

Do đó hàm số liên tục tại .

1. b) Dựa vào đồ thị hàm số ta thấy:

Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị .

1. b) Dựa vào đồ thị hàm số ta thấy:

Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị .

• Hàm số được gọi là liên tục trên khoảng  nếu hàm số liên tục tại mọi điểm thuộc khoảng đó.
• Hàm số được gọi là liên tục trên đoạn  nếu hàm số đó liên tục trên khoảng  và .

Chú ý Khái niệm hàm số liên tục trên các tập hợp có dạng  được định nghĩa tương tự.

Nhận xét

Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.

Ví dụ 2

1. a) Hàm số có liên tục trên đoạn hay không?
2. b) Hàm số có liên tục trên khoảng hay không?
3. a) Với mỗi ta có: . Ta lại có: 
4. b) Hàm số không xác định tại nên hàm số không liên tục tại

Do   nên hàm số đã cho không liên tục trên khoảng .