Soạn giáo án điện tử toán 11 Cánh diều Chương 4 Bài 5: Hình lăng trụ và hình hộp

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC NGÀY HÔM NAY!

KHỞI ĐỘNG

Trong thực tiễn, ta thường gặp nhiều đồ dùng, vật thể gợi nên hình ảnh hình lăng trụ, hình hộp. Chẳng hạn: Khung lịch để bàn (Hình 68); Tháp đôi Puerta de Europa ở Madrid, Tây Ban Nha (Hình 69), …

Hình lăng trụ và hình hộp là hình như thế nào?

CHƯƠNG IV. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG.

BÀI 5. HÌNH LĂNG TRỤ VÀ HÌNH HỘP

NỘI DUNG BÀI HỌC

1. HÌNH LĂNG TRỤ
2. Định nghĩa

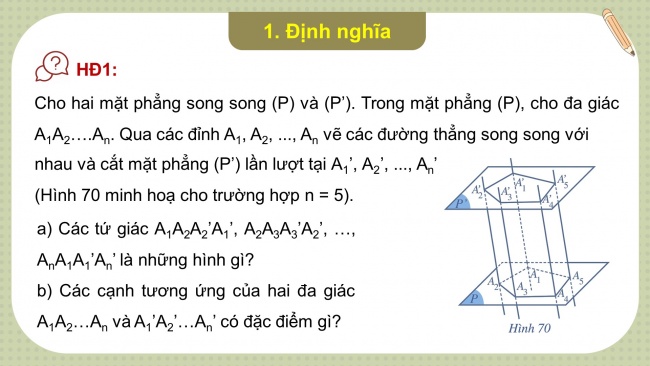
Cho hai mặt phẳng song song (P) và (P’). Trong mặt phẳng (P), cho đa giác A₁A₂….A_n. Qua các đỉnh A₁, A₂, ..., A_n vẽ các đường thẳng song song với

nhau và cắt mặt phẳng (P’) lần lượt tại A₁’, A₂­’, ..., A_n’ (Hình 70 minh hoạ cho trường hợp n = 5).

1. a) Các tứ giác A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, …, A_nA₁A₁’A_n’ là những hình gì?
2. b) Các cạnh tương ứng của hai đa giác A₁A₂…A_nvà A₁’A₂’…A_n’ có đặc điểm gì?
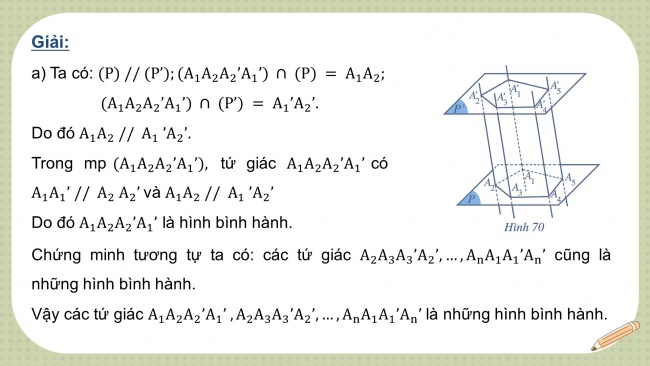
3. a) Ta có:

Do đó

Trong mp tứ giác có và

Do đó  là hình bình hành.

Chứng minh tương tự ta có: các tứ giác  cũng là những hình bình hành.

Vậy các tứ giác  là những hình bình hành.

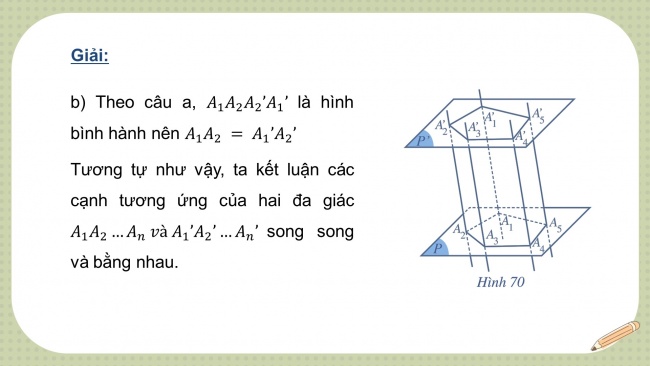
1. b) Theo câu a, là hình bình hành nên

Tương tự như vậy, ta kết luận các cạnh tương ứng của hai đa giác song song và bằng nhau.

ĐỊNH NGHĨA

Hình gồm các đa giác  và các hình bình hành được gọi là hình lăng trụ, kí hiệu là .

CHÚ Ý

Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,... thì hình lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác,...

Trong hình lăng trụ

• Hai đa giác và  được gọi là hai mặt đáy;
• Các hình bình hành gọi là các mặt bên;
• Các cạnh của mặt hai mặt đấy gọi là các cạnh đáy;
• Các đoạn thẳng gọi là các cạnh bên;
• Các đỉnh của hai mặt đáy gọi là các đỉnh của hình lăng trụ.

2. Tính chất

Từ định nghĩa hình lăng trụ, nhận xét đặc điểm các mặt bên, cạnh bên và hai mặt đáy của hình lăng trụ.

Từ định nghĩa hình lăng trụ, ta có các nhận xét sau:

• Các cạnh bên của hình lăng trụ song song và bằng nhau.
• Các mặt bên của hình lăng trụ là các hình bình hành.
• Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.

KẾT LUẬN

• Các cạnh bên của hình lăng trụ song song và bằng nhau.
• Các mặt bên của hình lăng trụ là các hình bình hành.
• Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Ví dụ 1

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’. Chứng minh rằng:

1. a) AA' // (BCC'B'); b) AM // A'M'.
2. a) Trong hình lăng trụ ABC.A’B’C’, ta có: AA’ // BB’ và BB’ (BCC’B’), suy ra AA’ // (BCC’B’).
3. b) Vì MM’ // BB’, MM’ = BB’ và BB’ // AA’, BB’ = AA’ nên MM’ // AA’, MM’ = AA’.

Suy ra AMM’A’ là hình bình hành. Vậy AM // A’M’.

LUYỆN TẬP 1

Cho một số ví dụ về những đồ dùng, vật thể trong thực tế có dạng hình lăng trụ.

1. HÌNH HỘP
2. Định nghĩa

Vẽ hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành.

Hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành:

          Hãy liệt kê các cặp mặt đối diện, các cặp cạnh đối diện và các cặp đỉnh đối diện của hình hộp ABCD.A’B’C’D’ (Hình 73).

Trong hình hộp ABCD.A’B’C’D’, ta có:

- Ba cặp mặt đối diện: (ABCD) và (A’B’C’D’); (ABB’A’) và (DCC’D’); (ADD’A’)

và (BCC’B’).

- Sáu cặp cạnh đối diện: AB và D’C’; BC và A’D’; CD và B’A’; DA và C’B’; AA’ và CC’; BB’ và DD’.

- Bốn cặp đỉnh đối diện: A và C’; B và D’; C và A’; D và B’.