Soạn giáo án điện tử toán 11 Cánh diều Chương 6 Bài 3: Hàm số mũ. Hàm số lôgarit

Nội dung giáo án

THÂN MẾN CHÀO ĐÓN CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

Một doanh nghiệp gửi ngân hàng 1 tỉ đồng với kì hạn 1 năm, lãi suất /năm. Giả sử trong suốt  năm , doanh nghiệp đó không rút tiền ra và số tiền lãi sau mỗi năm sẽ được nhập vào vốn ban đầu. Biết rằng lãi suất không thay đổi trong thời gian này.

Mối liên hệ giữa số tiền doanh nghiệp đó có được (cả gốc và lãi) với số năm gửi ngân hàng gợi nên hàm số nào trong toán học?

CHƯƠNG VI: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT

BÀI 3. HÀM SỐ MŨ.

HÀM SỐ LÔGARIT

NỘI DUNG BÀI HỌC

Hàm số mũ

Hàm số lôgarit

1. HÀM SỐ MŨ
2. Định nghĩa

HĐ1

Xét bài toán ở phần mở đầu.

1. a) Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm;
2. b) Dự đoán công thức tính số tiền doanh nghiệp đó có được sau năm.

Giải

1. a) Số tiền doanh nghiệp đó có được:

• Sau 1 năm:

 (đồng)

• Sau 2 năm:

 (đồng)

• Sau 3 năm:

1. b) Dự đoán công thức:

NHẬN XÉT

Tương ứng mỗi giá trị  với giá trị  xác định một hàm số, hàm số đó gọi là hàm số mũ cơ số .

Kết luận

Cho số thực  . Hàm số  được gọi là hàm số mũ cơ số .

Tập xác định của hàm số mũ  là .

Ví dụ 1

Trong các hàm số sau hàm số nào là hàm số mũ

Giải:

Trong các hàm số đã cho, chỉ có hàm số  là có dạng   với  nên  là hàm số mũ.

LUYỆN TẬP 1

Cho hai ví dụ về hàm số mũ.

Gợi ý

2. Đồ thị và tính chất

HĐ2

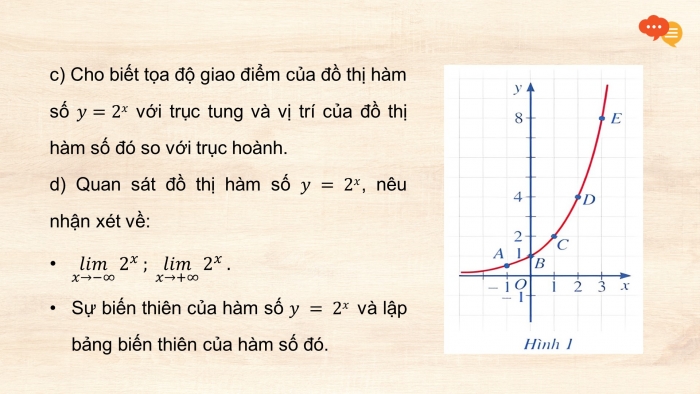
Cho hàm số mũ

1. a) Tìm giá trị tương ứng với giá trị của trong bảng sau:
2. b) Trong mặt phẳng tọa độ , hãy biểu diễn các điểm trong bảng giá trị ở câu a.

Bằng cách làm tương tự, lấy nhiều điểm với và nối lại, ta được đồ thị hàm số (Hình 1).

1. c) Cho biết tọa độ giao điểm của đồ thị hàm số với trục tung và vị trí của đồ thị hàm số đó so với trục hoành.
2. d) Quan sát đồ thị hàm số , nêu nhận xét về:

• Sự biến thiên của hàm số và lập bảng biến thiên của hàm số đó.

Giải

1. b) Các điểm

được biểu diễn trên mặt phẳng tọa độ  như Hình 1.

1. c) Tọa độ giao điểm của đồ thị với trục tung là . Đồ thị không cắt trục hoành.

Giải

Nhận xét: Đồ thị hàm số  là một đường cong liền nét, cắt trục tung tại điểm có tung độ bằng 1, nằm ở phía trên trục hoành và đi lên từ trái sang phải.