Soạn giáo án điện tử toán 11 Cánh diều Chương 3 Bài 1: Giới hạn của dãy số

Nội dung giáo án

CHÀO MỪNG TẤT CẢ CÁC EM
ĐẾN VỚI BÀI HỌC HÔM NAY!

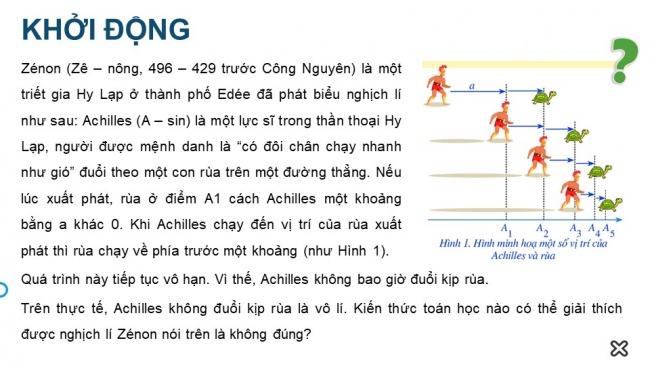
KHỞI ĐỘNG Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp, người được mệnh danh là “có đôi chân chạy nhanh như gió” đuổi theo một con rùa trên một đường thẳng. Nếu lúc xuất phát, rùa ở điểm A1 cách Achilles một khoảng bằng a khác 0. Khi Achilles chạy đến vị trí của rùa xuất phát thì rùa chạy về phía trước một khoảng (như Hình 1).

Trên thực tế, Achilles không đuổi kịp rùa là vô lí. Kiến thức toán học nào có thể giải thích được nghịch lí Zénon nói trên là không đúng?

CHƯƠNG III. GIỚI HẠN.

HÀM SỐ LIÊN TỤC

BÀI 1. GIỚI HẠN CỦA DÃY SỐ

NỘI DUNG BÀI HỌC

GIỚI HẠN HỮU HẠN CỦA DÃY SỐ

1. Định nghĩa

HĐ1

Hình 2 biểu diễn các số hạng của dãy số với  trên hệ trục toạ độ

1. a) Nhận xét về sự thay đổi các giá trị khi ngày càng lớn.

Khi n ngày càng lớn thì giá trị của càng giảm dần về 0.

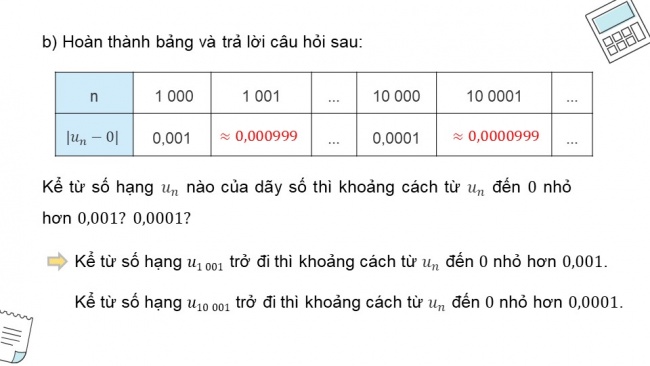
1. b) Hoàn thành bảng và trả lời câu hỏi sau:

Kể từ số hạng  nào của dãy số thì khoảng cách từ  đến  nhỏ hơn

Kể từ số hạng  trở đi thì khoảng cách từ  đến  nhỏ hơn .

Kể từ số hạng  trở đi thì khoảng cách từ  đến  nhỏ hơn .

Kể từ số hạng  trở đi thì khoảng cách từ  đến  nhỏ hơn .

Kể từ số hạng  trở đi thì khoảng cách từ  đến  nhỏ hơn .

Dãy số  có giới hạn 0 khi  dần tới dương vô cực nếu  có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu .

Chú ý

Ngoài kí hiệu , ta cũng sử dụng các kí hiệu sau:

 hay  khi  

Từ Hoạt động 1, ta có:  

Nhận xét:

Nếu  ngày càng gần tới 0 khi  ngày càng lớn thì

Ví dụ 1: Cho dãy số  với . Giả sử  là số dương bé tuỳ ý cho trước.

1. a) Tìm số tự nhiên để
2. b) Tính
3. a) Ta có . Do đó:

Vậy với các số tự nhiên  lớn hơn  thì .

1. b) Theo định nghĩa về dãy số có giới hạn 0, ta có

LUYỆN TẬP 1

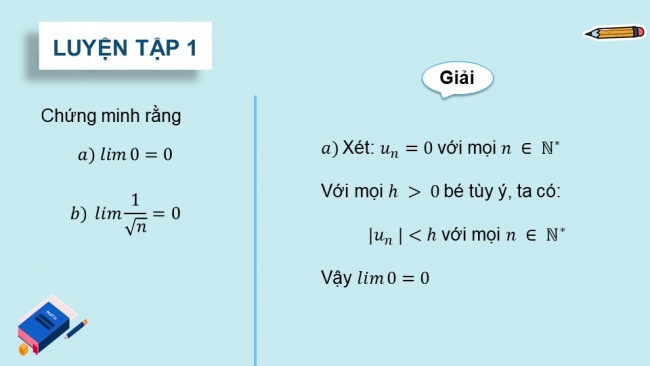
Chứng minh rằng

Xét: với mọi

Với mọi bé tùy ý, ta có:

 với mọi

Vậy